题目内容
(1)求值sin2840°+cos540°+tan225°-cos2(-330°)+sin(-210°)
(2)已知
=3,计算:
.
(2)已知
| 1+tana |
| 1-tana |
| 2sina-3cosa |
| 4sina-9cosa |
分析:(1)根据诱导公式,我们可将sin2840°+cos540°+tan225°-cos2(-330°)+sin(-210°)化为sin2120°+cos180°+tan45°-cos230°+sin150°,代入各特殊角的三角函数值,即可求出答案.
(2)由
=3,我们可计算出tanα的值,由于
是齐次分式,弦化切后,即可得到答案.
(2)由
| 1+tana |
| 1-tana |
| 2sina-3cosa |
| 4sina-9cosa |
解答:解:(1)原式=sin2120°+cos180°+tan45°-cos230°+sin150°
=(
)2-1+1-(
)2+
…(4分)
=
…(6分)
(2)解:∵
=3
∴tanα=
…(8分)
∴
=
=
…(12分)
=(
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
(2)解:∵
| 1+tanα |
| 1-tanα |
∴tanα=
| 1 |
| 2 |
∴
| 2sinα-3cosα |
| 4sinα-9cosα |
| 2tanα-3 |
| 4tanα-9 |
| 2 |
| 7 |
点评:本题考查的知识点是三角函数的恒等变换及化简求值,同角三角函数间的基本关系,其中(1)的关键是利用诱导公式,将角变到0°~180°之间,而(2)的关键是对齐次分式弦化切.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
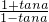 =3,计算:
=3,计算: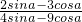 .
.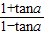 =3,计算:
=3,计算: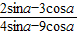 .
.