题目内容
(本题满分12分)已知圆 ,点
,点 是圆内的任意一点,直线
是圆内的任意一点,直线 .
.
(1)求点 在第一象限的概率
在第一象限的概率 ;
;
(2)若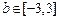 ,求直线
,求直线 与
与 圆
圆 相交的概率.
相交的概率.
 ,点
,点 是圆内的任意一点,直线
是圆内的任意一点,直线 .
. (1)求点
 在第一象限的概率
在第一象限的概率 ;
;(2)若
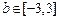 ,求直线
,求直线 与
与 圆
圆 相交的概率.
相交的概率.解:(1)设圆 与
与 轴的交点为
轴的交点为 。连结
。连结 .
.
令 中的
中的 得
得 ,
,
所以 ,因为
,因为 ,所以
,所以 ,
,
所以圆在 轴左侧的弓形的面积为
轴左侧的弓形的面积为 ,
,
所以圆面在第一象限部分的面积为 .
.
所以,点 在第一象限的概率
在第一象限的概率 .……………7分
.……………7分
(2 )欲使直线
)欲使直线 与圆
与圆 相交,须满足
相交,须满足 ,
,
即 ,解得
,解得 . 又因为
. 又因为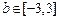 ,
,
所以直线 与圆
与圆 相交的概率
相交的概率
 .………………14分
.………………14分
 与
与 轴的交点为
轴的交点为 。连结
。连结 .
.令
 中的
中的 得
得 ,
,所以
 ,因为
,因为 ,所以
,所以 ,
,所以圆在
 轴左侧的弓形的面积为
轴左侧的弓形的面积为 ,
,所以圆面在第一象限部分的面积为
 .
.所以,点
 在第一象限的概率
在第一象限的概率 .……………7分
.……………7分(2
 )欲使直线
)欲使直线 与圆
与圆 相交,须满足
相交,须满足 ,
,即
 ,解得
,解得 . 又因为
. 又因为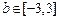 ,
,所以直线
 与圆
与圆 相交的概率
相交的概率
 .………………14分
.………………14分略

练习册系列答案
相关题目
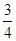 ,谁能将铜板整个扔到方几上,就可以进行下一轮比赛。郭靖一扔,铜板落在小方几上,且没有掉下,问他能进入下一轮比赛的概率多大? ( )
,谁能将铜板整个扔到方几上,就可以进行下一轮比赛。郭靖一扔,铜板落在小方几上,且没有掉下,问他能进入下一轮比赛的概率多大? ( )

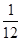

 ,战胜美国队的概率为
,战胜美国队的概率为 ,两场比赛的胜负相互独立;则中国队在与日本队和美国队的比赛中,恰好胜一场的概率是
,两场比赛的胜负相互独立;则中国队在与日本队和美国队的比赛中,恰好胜一场的概率是



 、
、 、
、 、
、 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.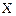 饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求 两点有5条连线并联,它们在单位时间内能通过的信息量依次为
两点有5条连线并联,它们在单位时间内能通过的信息量依次为 .现从中任取三条线且记在单位时间内通过的信息总量为
.现从中任取三条线且记在单位时间内通过的信息总量为 .
.

 和
和 ,则复数
,则复数 (
( 是虚数单位)为实数的概率 (结果用最简分数表示)
是虚数单位)为实数的概率 (结果用最简分数表示)