题目内容
已知曲线 的参数方程为
的参数方程为 为参数),在平面直角坐标系中,以坐标原点为极点,
为参数),在平面直角坐标系中,以坐标原点为极点, 轴的非负半轴极轴建立极坐标系,曲线
轴的非负半轴极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,求
,求 与
与 交点的极坐标,其中
交点的极坐标,其中
 与
与 交点的极坐标分别为
交点的极坐标分别为 或
或 .
.
【命题立意】本题旨在考查参数方程与极坐标方程、直角坐标方程的转化与应用.
【解析】解法一:将 消去参数
消去参数 ,得
,得 ,
,
所以 的普通方程为:
的普通方程为: . ……………………4分
. ……………………4分
将曲线 的极坐标方程化为直角坐标方程得:
的极坐标方程化为直角坐标方程得: . …………………6分
. …………………6分
由 解得
解得 或
或 ……………………8分
……………………8分
所以 与
与 交点的极坐标分别为
交点的极坐标分别为 或
或 . …………………10分
. …………………10分
解法二:将 消去参数
消去参数 ,得
,得 ,
,
所以 的普通方程为:
的普通方程为: . …………………………4分
. …………………………4分
所以 的极坐标方程为
的极坐标方程为 . …………………………6分
. …………………………6分
代入 ,得
,得 , ………………………………8分
, ………………………………8分

练习册系列答案
相关题目
 中,已知向量
中,已知向量 ,
, ,
, 。
。 ,求tan x的值 (2)若
,求tan x的值 (2)若 与
与 的夹角为
的夹角为 ,求
,求 的值。
的值。 ,
, B.
B. ,
, D.
D.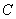 的极坐标方程为
的极坐标方程为 .以极点为原点,极轴为
.以极点为原点,极轴为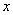 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线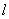 的参数方程为
的参数方程为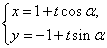 (
(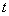 为参数).
为参数).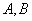 两点,且
两点,且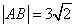 ,求直线
,求直线 ,则线段
,则线段 的长度是( )
的长度是( ) C.7 D.5
C.7 D.5
 是
是 的外接圆,
的外接圆, ,
, 是
是 边上的高,
边上的高, 是圆
是圆 作圆
作圆 的延长线于点
的延长线于点 .
. ;
; ,
, ,求
,求
 的解集为 .
的解集为 . ],且sin θ=
],且sin θ= ,则tan
,则tan  =________.
=________.