题目内容
.在△ABC中,已知内角 ,边
,边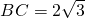 ,设内角B=x,面积为y
,设内角B=x,面积为y
(1)求函数y=f(x)的解析式
(2)求y的最值.
解:(1)∵内角 ,边
,边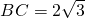 ,内角B=x
,内角B=x
∴由正弦定理可得
∴AB=4sin( )
)
∴面积y= •4sin(
•4sin( )•
)• sinx=4
sinx=4 (
( )sinx=2
)sinx=2 sin(2x-
sin(2x- )+
)+
(2)∵0<x< ,∴-
,∴- <2x-
<2x- <
<
∴- <sin(2x-
<sin(2x- )≤1
)≤1
∴0<2 sin(2x-
sin(2x- )+
)+ ≤3
≤3
∴2x- =
= ,即x=
,即x= 时,y取得最大值3
时,y取得最大值3 .
.
分析:(1)利用正弦定理,求出AB,再利用三角形的面积公式,即可求函数y=f(x)的解析式
(2)利用辅助角公式,将函数的解析式,化为正弦型函数的形式,再根据正弦型函数的最值的求法进行求解.
点评:本题考查正弦定理的运用,考查三角函数的化简,考查学生的计算能力,属于中档题.
 ,边
,边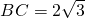 ,内角B=x
,内角B=x∴由正弦定理可得

∴AB=4sin(
 )
)∴面积y=
 •4sin(
•4sin( )•
)• sinx=4
sinx=4 (
( )sinx=2
)sinx=2 sin(2x-
sin(2x- )+
)+
(2)∵0<x<
 ,∴-
,∴- <2x-
<2x- <
<
∴-
 <sin(2x-
<sin(2x- )≤1
)≤1∴0<2
 sin(2x-
sin(2x- )+
)+ ≤3
≤3
∴2x-
 =
= ,即x=
,即x= 时,y取得最大值3
时,y取得最大值3 .
.分析:(1)利用正弦定理,求出AB,再利用三角形的面积公式,即可求函数y=f(x)的解析式
(2)利用辅助角公式,将函数的解析式,化为正弦型函数的形式,再根据正弦型函数的最值的求法进行求解.
点评:本题考查正弦定理的运用,考查三角函数的化简,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目