题目内容
已知复数ω满足ω=2-i(i为虚数单位),复数z= +|ω-2|,则一个以z为根的实系数一元二次方程是( )
+|ω-2|,则一个以z为根的实系数一元二次方程是( )A.x2+6x+10=0
B.x2-6x+10=0
C.x2+6x-10=0
D.x2-6x-10=0
【答案】分析:利用复数的运算性质可求得z=3+i,代入所求的一元二次方程x2+px+q=0,利用两复数相等的充要条件解得p与q的值即可.
解答:解:∵ω=2-i,
∴z=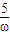 +|ω-2|=2+i+1=3+i,
+|ω-2|=2+i+1=3+i,
又z为实系数一元二次方程x2+px+q=0的根,
∴(3+i)2+p(3+i)+q=0,
∴8+3p+q=0,p+6=0,
∴p=-6,q=10.
∴该一元二次方程为:x2-6x+10=0.
故选B.
点评:本题考查复数代数形式的混合运算,求得z=3+i是关键,考查理解与解方程组的能力,属于中档题.
解答:解:∵ω=2-i,
∴z=
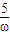 +|ω-2|=2+i+1=3+i,
+|ω-2|=2+i+1=3+i,又z为实系数一元二次方程x2+px+q=0的根,
∴(3+i)2+p(3+i)+q=0,
∴8+3p+q=0,p+6=0,
∴p=-6,q=10.
∴该一元二次方程为:x2-6x+10=0.
故选B.
点评:本题考查复数代数形式的混合运算,求得z=3+i是关键,考查理解与解方程组的能力,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 满足
满足 =2,则
=2,则 的最大值为 .
的最大值为 . 满足
满足 =2,则
=2,则 的最大值为 .
的最大值为 . 满足
满足 =2,则
=2,则 的最大值为 .
的最大值为 .