题目内容
 角α的终边OP与单位圆的交点为P(m,n),
角α的终边OP与单位圆的交点为P(m,n),(1)填空:sinα=
(2)点Q(x,y)在射线OP上,设点Q(x,y)到原点的距离为r=|OQ|,利用三角形知识求证:
| y | r |
分析:(1)显然单位圆的半径等于零,再根据正弦函数和余弦函数在坐标系中的定义,可以算得sinα=n,cosα=m,
(2)作出辅助线:作PM⊥x轴,QN⊥x轴,垂足为M、N,则PM∥QN,根据图中的PM与QN相互平行,可以得到△OPM\~△OQN,从而得到线段成比例:
=
,再代入题中所给的数据,可得
=n成立.
(2)作出辅助线:作PM⊥x轴,QN⊥x轴,垂足为M、N,则PM∥QN,根据图中的PM与QN相互平行,可以得到△OPM\~△OQN,从而得到线段成比例:
| QN |
| OQ |
| PM |
| OP |
| y |
| r |
解答:解:(1)根据三角函数在坐标系里的定义,若点M(x,y),OM=
则sinα=
,cosα=
,
因此sinα=n,cosα=m,
(2)作PM⊥x轴,QN⊥x轴,垂足为M、N,则PM∥QN,
∴△OPM\~△OQN,
∴
=
=
=
=n.
| x2+y2 |
则sinα=
| y |
| r |
| x |
| r |
因此sinα=n,cosα=m,
(2)作PM⊥x轴,QN⊥x轴,垂足为M、N,则PM∥QN,
∴△OPM\~△OQN,
∴
| y |
| r |
| QN |
| OQ |
| PM |
| OP |
| n |
| 1 |
点评:本题主要考查二次函数函数定区间上求最值问题,以点关于直线的对称点与向量的数量积等问题,此题是一道综合性较强的题型,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P,Q,已知点P的坐标为
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于点P,Q,已知点P的坐标为 角α的终边OP与单位圆的交点为P(m,n),
角α的终边OP与单位圆的交点为P(m,n), .(只考虑第一象限)
.(只考虑第一象限)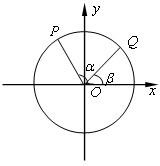
 .(只考虑第一象限)
.(只考虑第一象限)