题目内容
已知椭圆
的离心率为
，长轴长为2
．
（1）求椭圆的方程；
（2）试直线y=kx+1交椭圆于不同的两点A、B，以AB为直径的圆恰过原点O，求直线方程．
解：（1）设椭圆的半焦距为c，
∵椭圆的离心率为，长轴长为2
∴
，
∴
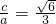
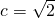
∵a2=b2+c2
∴b=1 （2分）
∴所求椭圆方程为
（4分）
（2）设A（x1，y1），B（x2，y2），
由
消去y并整理得（1+3k2）x2+6kx=0
则△=（6k）2-4（1+3k2）×0＞0，
解得k≠0 （5分）
故
，x1x2=0 （8分）
∵以AB为直径的圆恰过原点O
∴
∴x1x2+y1y2=x1x2+（kx1+1）（kx2+1）=（1+k2）x1x2+k（x1+x2）+1=
（10分）．
∴
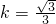
∴直线方程为
（12分）
分析：（1）根据椭圆的几何性质，求出几何量，即可得到椭圆的方程；
（2）直线方程与椭圆方程联立，利用韦达定理结合以AB为直径的圆恰过原点O，求得切线向量，即可求得直线方程．
点评：本题重点考查椭圆的标准方程，考查直线与椭圆的位置关系，解题的关键是借助于韦达定理，将以AB为直径的圆恰过原点O，转化为．
∵椭圆
的离心率为，长轴长为2∴
，∴
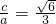
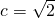
∵a2=b2+c2
∴b=1 （2分）
∴所求椭圆方程为
（4分）（2）设A（x1，y1），B（x2，y2），
由
消去y并整理得（1+3k2）x2+6kx=0
则△=（6k）2-4（1+3k2）×0＞0，
解得k≠0 （5分）
故
，x1x2=0 （8分）∵以AB为直径的圆恰过原点O
∴
∴x1x2+y1y2=x1x2+（kx1+1）（kx2+1）=（1+k2）x1x2+k（x1+x2）+1=
（10分）． ∴
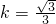
∴直线方程为
（12分）分析：（1）根据椭圆的几何性质，求出几何量，即可得到椭圆的方程；
（2）直线方程与椭圆方程联立，利用韦达定理结合以AB为直径的圆恰过原点O，求得切线向量，即可求得直线方程．
点评：本题重点考查椭圆的标准方程，考查直线与椭圆的位置关系，解题的关键是借助于韦达定理，将以AB为直径的圆恰过原点O，转化为
． 
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知椭圆的离心率为e，两焦点分别为F1、F2，抛物线C以F1为顶点、F2为焦点，点P为抛物线和椭圆的一个交点，若e|PF2|=|PF1|，则e的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
，焦点是（-3，0），（3，0），则椭圆方程为（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在由圆O：x2+y2=1和椭圆C：
如图，A，B是椭圆C：