题目内容
已知二次函数
的导数为
，
，对于任意实数
都有
，则
的最小值为（ ）
| A．3 | B． | C．2 | D． |
C
解析试题分析：对于任意实数都有，所以
，，所以
，所以
考点：本小题主要考查导数的计算、二次函数的图象和性质以及利用基本不等式求最值，考查学生的分析问题、解决问题的能力.
点评：利用基本不等式求最值，关键是要满足“一正二定三相等”三个条件.
练习册系列答案
相关题目
，则
的大小关系是
A． | B． | C． | D． |
若
，则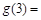
（ ）
A． | B． | C． | D． |
对任意
，函数
不存在极值点的充要条件是（ ）
A． 或 | B． |
C． | D． 或 |
幂指函数
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
，于是
。运用此方法可以探求得知
的一个单调递增区间为（ ）
| A．(0,2) | B．(2,3) | C．(e,4) | D．(3,8) |
若
，则（ ）
A． | B． |
C． | D． |
设
，则
的解集为
A． | B． | C． | D． |
若关于x的方程
（a>0，且
）有解，则m的取值范围是（ ）
A． | B． | C． | D． |
若幂函数
的图像不过原点,且关于原点对称,
则
的取值是
A． | B． |
C． | D． |