Question

求证：对角互补的四边形，必定内接于圆.

Answer 1

证明：改证它的逆否命题：“若四边形不内接于圆，则它的对角不互补.”

    如图（1）、图（2）所示，由于四边形ABCD不内接于圆，那么过不在一直线上的三点A、B、C所作的圆不能通过点D，这时，点D或在圆内或在圆外，没有其他可能.

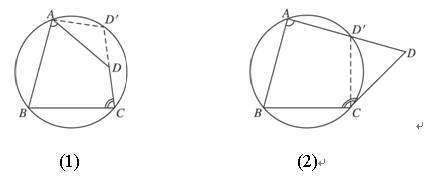
若点D在圆内，如图（1），延长CD至圆上的点D′，连结AD′，则有∠D′AB+∠C=180°,

而∠D′AB＞∠DAB,

∴∠DAB+∠C＜180°.

因而∠ADC+∠B＞180°.

故四边形ABCD的对角不互补.

同理，可证若点D在圆外时四边形ABCD的对角不互补.

∴原命题成立.