题目内容
已知椭圆 的离心率为
的离心率为 ,且曲线过点
,且曲线过点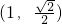
(1)求椭圆C的方程.(2)已知直线x-y+m=0与椭圆C交于不同的两点A,B,且线段AB的中点不在圆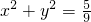 内,求m的取值范围.
内,求m的取值范围.
解:(1)∵ ,∴
,∴ ,∴a2=2b2①
,∴a2=2b2①
曲线过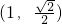 ,则
,则 ②
②
由①②解得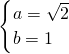 ,则椭圆方程为
,则椭圆方程为 .
.
(2)联立方程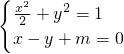 ,消去y整理得:3x2+4mx+2m2-2=0
,消去y整理得:3x2+4mx+2m2-2=0
则△=16m2-12(2m2-2)=8(-m2+3)>0,解得 ③
③
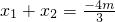 ,
, ,
,
即AB的中点为
又∵AB的中点不在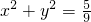 内,
内,
∴
解得,m≤-1或m≥1④
由③④得: <m≤-1或1≤m<
<m≤-1或1≤m< .
.
分析:(1)根据离心率为 ,a2=b2+c2得到关于a和b的一个方程,曲线过点
,a2=b2+c2得到关于a和b的一个方程,曲线过点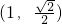 ,把点代入方程即可求得椭圆C的方程;
,把点代入方程即可求得椭圆C的方程;
(2)直线x-y+m=0与椭圆C交于不同的两点A,B,且线段AB的中点,联立直线和椭圆的方程,消元,得到关于x的一元二次方程,利用韦达定理求得AB的中点坐标,再根据该点不在圆内,得到该点到圆心的距离≥半径,求得m的取值范围.
点评:本小题主要考查直线与圆锥曲线等基础知识,考查数形结合的数学思想方法,以及推理论证能力、运算求解能力,直线与圆锥曲线相交问题,易忽视△>0,属中档题.
 ,∴
,∴ ,∴a2=2b2①
,∴a2=2b2①曲线过
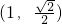 ,则
,则 ②
②由①②解得
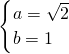 ,则椭圆方程为
,则椭圆方程为 .
.(2)联立方程
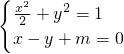 ,消去y整理得:3x2+4mx+2m2-2=0
,消去y整理得:3x2+4mx+2m2-2=0则△=16m2-12(2m2-2)=8(-m2+3)>0,解得
 ③
③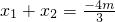 ,
, ,
,即AB的中点为

又∵AB的中点不在
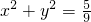 内,
内,∴

解得,m≤-1或m≥1④
由③④得:
 <m≤-1或1≤m<
<m≤-1或1≤m< .
.分析:(1)根据离心率为
 ,a2=b2+c2得到关于a和b的一个方程,曲线过点
,a2=b2+c2得到关于a和b的一个方程,曲线过点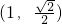 ,把点代入方程即可求得椭圆C的方程;
,把点代入方程即可求得椭圆C的方程;(2)直线x-y+m=0与椭圆C交于不同的两点A,B,且线段AB的中点,联立直线和椭圆的方程,消元,得到关于x的一元二次方程,利用韦达定理求得AB的中点坐标,再根据该点不在圆内,得到该点到圆心的距离≥半径,求得m的取值范围.
点评:本小题主要考查直线与圆锥曲线等基础知识,考查数形结合的数学思想方法,以及推理论证能力、运算求解能力,直线与圆锥曲线相交问题,易忽视△>0,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: