题目内容
已知以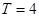 为周期的函数
为周期的函数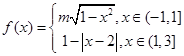 ,其中
,其中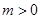 。若方程
。若方程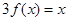 恰有5个实数解,则
恰有5个实数解,则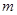 的取值范围为
的取值范围为
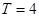 为周期的函数
为周期的函数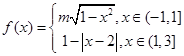 ,其中
,其中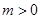 。若方程
。若方程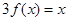 恰有5个实数解,则
恰有5个实数解,则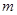 的取值范围为
的取值范围为 A.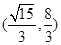 | B.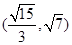 | C.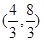 | D.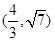 |
B
∵当x∈(﹣1,1]时,将函数化为方程x2+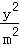 =1(y≥0),
=1(y≥0),
∴实质上为一个半椭圆,其图象如图所示,
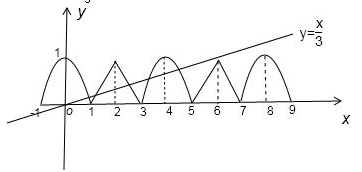
同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,
由图易知直线 y=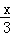 与第二个椭圆(x﹣4)2+
与第二个椭圆(x﹣4)2+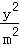 =1(y≥0)相交,
=1(y≥0)相交,
而与第三个半椭圆(x﹣8)2+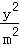 ="1" (y≥0)无公共点时,方程恰有5个实数解,
="1" (y≥0)无公共点时,方程恰有5个实数解,
将 y=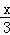 代入(x﹣4)2+
代入(x﹣4)2+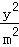 ="1" (y≥0)得,(9m2+1)x2﹣72m2x+135m2=0,令t=9m2(t>0),
="1" (y≥0)得,(9m2+1)x2﹣72m2x+135m2=0,令t=9m2(t>0),
则(t+1)x2﹣8tx+15t=0,由△=(8t)2﹣4×15t (t+1)>0,得t>15,由9m2>15,且m>0得 m ,
,
同样由 y=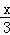 与第三个椭圆(x﹣8)2+
与第三个椭圆(x﹣8)2+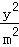 ="1" (y≥0)由△<0可计算得 m<
="1" (y≥0)由△<0可计算得 m<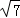 ,
,
综上可知m∈(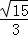 ,
,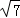 )
)
故选B
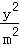 =1(y≥0),
=1(y≥0),∴实质上为一个半椭圆,其图象如图所示,

同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,
由图易知直线 y=
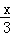 与第二个椭圆(x﹣4)2+
与第二个椭圆(x﹣4)2+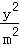 =1(y≥0)相交,
=1(y≥0)相交,而与第三个半椭圆(x﹣8)2+
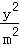 ="1" (y≥0)无公共点时,方程恰有5个实数解,
="1" (y≥0)无公共点时,方程恰有5个实数解,将 y=
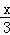 代入(x﹣4)2+
代入(x﹣4)2+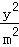 ="1" (y≥0)得,(9m2+1)x2﹣72m2x+135m2=0,令t=9m2(t>0),
="1" (y≥0)得,(9m2+1)x2﹣72m2x+135m2=0,令t=9m2(t>0),则(t+1)x2﹣8tx+15t=0,由△=(8t)2﹣4×15t (t+1)>0,得t>15,由9m2>15,且m>0得 m
 ,
,同样由 y=
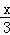 与第三个椭圆(x﹣8)2+
与第三个椭圆(x﹣8)2+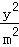 ="1" (y≥0)由△<0可计算得 m<
="1" (y≥0)由△<0可计算得 m<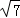 ,
,综上可知m∈(
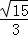 ,
,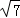 )
)故选B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
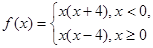 则函数
则函数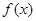 ( )
( )
 的图像经过怎样的平移得来;
的图像经过怎样的平移得来; ,求函数
,求函数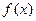 的最大值和最小值。
的最大值和最小值。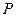 的关系近似地满足:
的关系近似地满足: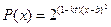 (其中
(其中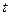 为关税的税率,且
为关税的税率,且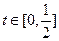 ,
,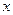 为市场价格,
为市场价格, 为正常数),当
为正常数),当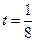 时的市场供应量曲线如图所示;
时的市场供应量曲线如图所示;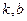 的值;
的值;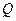 ,它近似满足
,它近似满足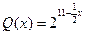 .
. 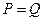 时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率
时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率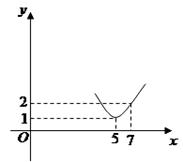
 是定义在
是定义在 上的函数,且对于任意的
上的函数,且对于任意的 ,有
,有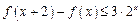 ,
, ,若
,若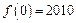 ,则
,则 ( )
( ) .
.
 .
.
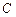 .
.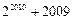
 .
.
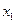 满足2x+
满足2x+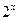 ="5,"
="5," 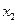 满足2x+2
满足2x+2 (x
(x 1)="5," 则
1)="5," 则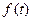 (单位:元/件)与时间t满足关系
(单位:元/件)与时间t满足关系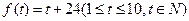 ,销售量
,销售量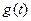 (单位:万件)与时间t满足关系
(单位:万件)与时间t满足关系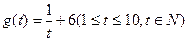 ,则这种商品的日销售额的最大值为 (万元)。
,则这种商品的日销售额的最大值为 (万元)。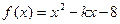 在[5,8]上是单调函数,则实数
在[5,8]上是单调函数,则实数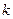 的取值范围是_____________
的取值范围是_____________ 一根为2,另一根为
一根为2,另一根为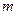 ,则
,则 ▲ .
▲ .