题目内容
7.已知函数f(x)=log3|x-t|是偶函数,记$a=f({{{log}_{0.3}}4}),b=f({\sqrt{π^3}}),c=f({2-t})$则a,b,c的大小关系为( )| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | c<b<a |
分析 由f(x)为偶函数,可得t=0,讨论x>0时,f(x)递增,化a=f(log0.30.25),运用指数函数和对数函数的单调性,比较π1.5、2、log0.30.25的大小,即可得到a,b,c的大小关系.
解答 解:函数f(x)=log3|x-t|是偶函数,
可得f(-x)=f(x),即log3|-x-t|=log3|x-t|,
即有|-x-t|=|x-t|恒成立,可得t=0,
则f(x)=log3|x|,当x>0时,f(x)=log3x为增函数,
a=f(log0.34)=f(log0.30.25),c=f(2-t)=f(2),
由1<log0.30.25<2,π1.5>π>3,
即有π1.5>2>log0.30.25,
则f(π1.5)>f(2)>f(log0.30.25),
即为b>c>a.
故选:A.
点评 本题考查函数的奇偶性和单调性的判断和应用:比较大小,注意运用定义法和转化思想,同时考查指数函数和对数函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
12.点M,N分别是正方体ABCD-A1B1C1D1的棱BB1和B1C1的中点,则MN和CD1所成角的大小为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
 如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=4,AC=2$\sqrt{7}$,DC=2
如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=4,AC=2$\sqrt{7}$,DC=2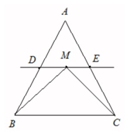 在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.
在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.