题目内容
1.下列四个命题中正确的是②③①sin2x+$\frac{4}{si{n}^{2}x}$的最小值是4
②若|x-2|<ε,|y-2|<ε,则|x-y|<2ε
③若函数f(x)=$\sqrt{{3}^{{x}^{2}-2ax-a}-1}$的定义域是R,则a的取值范围是[-1,0]
④过直线y=x上的一点做圆(x-5)2+(y-1)2=3的两条切线l1,l2,当直线l1,l2关于y=x对称时,他们之间的夹角为90°.
分析 换元后利用函数的单调性求出值域判断①;利用绝对值的不等式判断②;由函数的定义域为实数集求出a的范围判断③;数形结合求解得到l1,l2的夹角小于90°说明④错误.
解答 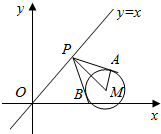 解:①令t=sin2x∈(0,1],则sin2x+$\frac{4}{si{n}^{2}x}$=$t+\frac{4}{t}$∈[5,+∞),①错误;
解:①令t=sin2x∈(0,1],则sin2x+$\frac{4}{si{n}^{2}x}$=$t+\frac{4}{t}$∈[5,+∞),①错误;
②由|x-2|<ε,|y-2|<ε,得|x-y|=|(x-2)-(y-2)|<|x-2|+|y-2|=2ε,②正确;
③由函数f(x)=$\sqrt{{3}^{{x}^{2}-2ax-a}-1}$的定义域是R,可知${3}^{{x}^{2}-2ax-a}-1≥0$对任意实数x都成立,
即${3}^{{x}^{2}-2ax-a}≥1={3}^{0}$,∴x2-2ax-a≥0对任意实数x恒成立,则△=(-2a)2+4a≤0,即a的取值范围是[-1,0],③正确;
④如图,过直线y=x上的一点做圆(x-5)2+(y-1)2=3的两条切线l1,l2,当直线l1,l2关于y=x对称时,
圆心M(5,1)到直线x-y=0的距离为MP=$\frac{|5-1|}{\sqrt{2}}=2\sqrt{2}$,半径MA=$\sqrt{3}$,
∴$sin∠MPA=\frac{\sqrt{3}}{2\sqrt{2}}=\frac{\sqrt{6}}{4}<\frac{\sqrt{2}}{2}$,∴l1,l2之间的夹角小于90°,④错误.
故答案为:②③.
点评 本题考查命题的真假判断与应用,考查了基本不等式的用法,考查直线和圆的位置关系的应用,属中档题.

练习册系列答案
相关题目
11.已知等差数列{an}满足a1+a2+a3+…+a101=0,则有( )
| A. | a1+a101>0 | B. | a2+a100<0 | C. | a3+a99=0 | D. | a51=51 |
6.已知f(x)是偶函数,且f(x+$\frac{1}{2}$)是奇函数,则下列结论不正确的是( )
| A. | f(x-1)是奇函数 | B. | f(x-$\frac{1}{2}$)是奇函数 | C. | f(x+1)是偶函数 | D. | f(x+2)偶函数 |