题目内容
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量α=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为 ( )
A.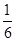 B.
B.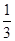 C.
C.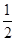 D.
D.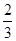
【答案】
B
【解析】
试题分析:由题意可知
 =(2,1),(2,3),(4,1),(4,3),从中取两个向量,基本事件总数为6,分别为(2,1)和(2,3);(2,1)和(4,1);(2,1)和(4,3);(2,3)和(4,1);(2,3)和(4,3);(4,1)和(4,3),其中,当所取的向量为(2,1)和(4,1);(2,1)和(4,3);(2,3)和(4,3)时,所得三角形
=(2,1),(2,3),(4,1),(4,3),从中取两个向量,基本事件总数为6,分别为(2,1)和(2,3);(2,1)和(4,1);(2,1)和(4,3);(2,3)和(4,1);(2,3)和(4,3);(4,1)和(4,3),其中,当所取的向量为(2,1)和(4,1);(2,1)和(4,3);(2,3)和(4,3)时,所得三角形 面积为1,所以
面积为1,所以
 ,选B,如图所示
,选B,如图所示

在图1中, ,在图2中,
,在图2中, ,选B.
,选B.
考点:1、向量;2、图形的面积;3、古典概型.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目