题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)过椭圆的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 、
、![]() ,其中直线
,其中直线![]() 交椭圆于
交椭圆于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于
于![]() 点,求证:直线
点,求证:直线![]() 平分线段
平分线段![]() .
.
【答案】(1) ![]() (2)见证明
(2)见证明
【解析】
(1)利用![]() ,得到
,得到![]() ,然后代入点
,然后代入点![]() 即可求解
即可求解
(2)设直线,以斜率![]() 为核心参数,与椭圆联立方程,把
为核心参数,与椭圆联立方程,把![]() 两点全部用参数
两点全部用参数![]() 表示,得出
表示,得出![]() 的中点坐标为
的中点坐标为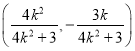 ,然后再求出直线
,然后再求出直线![]() 的方程,代入
的方程,代入![]() 的中点即可证明成立
的中点即可证明成立
(1)由![]() 得
得![]() ,所以
,所以![]()
由点![]() 在椭圆上得
在椭圆上得 解得
解得![]() ,
,
![]()
所求椭圆方程为![]()
(2)解法一:当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 平分线段
平分线段![]() 成立
成立
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程为
方程为![]() ,
,
联立方程得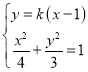 ,消去
,消去![]() 得
得![]()
因为![]() 过焦点,所以
过焦点,所以![]() 恒成立,设
恒成立,设![]() ,
,![]() ,
,
则![]() ,
,![]()
![]()
所以![]() 的中点坐标为
的中点坐标为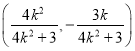
直线![]() 方程为
方程为![]() ,
,![]() ,可得
,可得![]() ,
,
所以直线![]() 方程为
方程为![]() ,
,
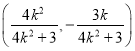 满足直线
满足直线![]() 方程,即
方程,即![]() 平分线段
平分线段![]()
综上所述,直线![]() 平分线段
平分线段![]()
(2)解法二:因为直线![]() 与
与![]() 有交点,所以直线
有交点,所以直线![]() 的斜率不能为0,
的斜率不能为0,
可设直线![]() 方程为
方程为![]() ,
,
联立方程得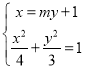 ,消去
,消去![]() 得
得![]()
因为![]() 过焦点,所以
过焦点,所以![]() 恒成立,设
恒成立,设![]() ,
,![]() ,
,
![]() ,
,![]()
![]()
所以![]() 的中点坐标为
的中点坐标为![]()
直线![]() 方程为
方程为![]() ,
,![]() ,由题可得
,由题可得![]() ,
,
所以直线![]() 方程为
方程为![]() ,
,
![]() 满足直线
满足直线![]() 方程,即
方程,即![]() 平分线段
平分线段![]()
综上所述,直线![]() 平分线段
平分线段![]()

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用电范围(度) | (0,210] | (210,400] |
|
某市随机抽取10户同一个月的用电情况,得到统计表如下:
居民用电户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用电量(度) | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯的部分每度0.8元,试计算A居民用电户用电410度时应电费多少元?
现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
以表中抽到的10户作为样本估计全市的居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.