题目内容
 如图:某地举行烟花燃放表演,观众席设置在地面线段OA,OB处.烟花燃放点在地面C处,现测得∠CBO=30°,∠BOC=∠OAC=45°,CO=50米,若点A,B离点C的距离相等,则OA的长度等于
如图:某地举行烟花燃放表演,观众席设置在地面线段OA,OB处.烟花燃放点在地面C处,现测得∠CBO=30°,∠BOC=∠OAC=45°,CO=50米,若点A,B离点C的距离相等,则OA的长度等于50
50
米.分析:在△COB中,由正弦定理求得 CB=50
=CA,设OA=x,△CAO中,由余弦定理可得502=(50
)2+x2-2x50
cos45°,解此一元二次方程求得x的值,即为所求.
| 2 |
| 2 |
| 2 |
解答:解:在△COB中,由正弦定理可得
=
,即
=
,解得 CB=50
(米),∴CA=50
(米).
设OA=x,△CAO中,由余弦定理可得 CO2=CA2+OA2-2CA•OA•cos∠OAC,
即 502=(50
)2+x2-2x50
cos45°,即 (x-50)2=0,解得 x=50(米),
故答案为50.
| CO |
| sin∠CBO |
| CB |
| sin∠BOC |
| 50 |
| sin30° |
| CB |
| sin45° |
| 2 |
| 2 |

设OA=x,△CAO中,由余弦定理可得 CO2=CA2+OA2-2CA•OA•cos∠OAC,
即 502=(50
| 2 |
| 2 |
故答案为50.
点评:本题主要考查正弦定理和余弦定理的应用,一元二次方程的解法,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 把正整数按一定的规则排成了如图所示的三角形数表.设
把正整数按一定的规则排成了如图所示的三角形数表.设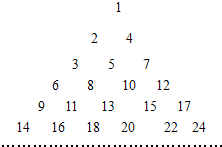 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8,a54=15.若aij=2011,则i与j的和为( )
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8,a54=15.若aij=2011,则i与j的和为( )