题目内容
把正整数按一定的规则排成了如图所示的三角形数表．设aij(i，j∈N*)是位于这个三角形数表中从上往下数第i行，从左往右数第j个数，若aij=2013，则i与j的和为（ ）分析：由三角形数表可以看出其奇数行为奇数列，偶数行为偶数列，前32个奇数行内数的个数的和为1024，得到2013在第32个奇数行内，且奇数从大到小排列，从而得到结果．
解答：解：由三角形数表可以看出其奇数行为奇数列，偶数行为偶数列，由2013=2×1007-1，得2013为第1007个奇数，
又前31个奇数行内数的个数的和为1+3+…+61=961，前32个奇数行内数的个数的和为1024，
故2013在第32个奇数行内，所以i=63，且奇数从大到小排列
因为第63行的第一个数为2×1024-1=2047，2013=2047-2（m-1），
所以m=18，即j=18，
所以i+j=81．
故选D
又前31个奇数行内数的个数的和为1+3+…+61=961，前32个奇数行内数的个数的和为1024，
故2013在第32个奇数行内，所以i=63，且奇数从大到小排列
因为第63行的第一个数为2×1024-1=2047，2013=2047-2（m-1），
所以m=18，即j=18，
所以i+j=81．
故选D
点评：本题考查简单的演绎推理，考查数列的特点，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
1、把正整数按一定的规则排成了如图所示的三角形数表．设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a42=8．若aij=2 009，则i与j的和为（ ）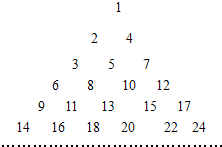
把正整数按一定的规则排成了如图所示的三角形数表．设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a42=8，a54=15．若aij=2011，则i与j的和为（ ）
把正整数按一定的规则排成了如图所示的三角形数表．设aij（i，j∈N+）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a42=8．若aij=2013，则i与j的和为（ ）
把正整数按一定的规则排成了如图所示的三角形数表，设（aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右第j个数，如 a42=8，若aij=2009，