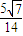题目内容
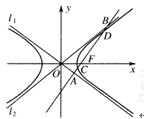
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率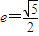 .
.(I)求证:
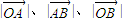 依次成等差数列;
依次成等差数列;(II)若
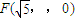 ,求直线AB在双曲线上所截得的弦CD的长度.
,求直线AB在双曲线上所截得的弦CD的长度.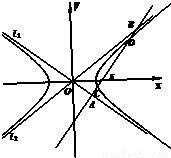
【答案】分析:(I)由双曲线的离心率求得a和c的关系,进而求得b和a的关系,设∠AOF=∠BOF=θ,则tanθ可求得,利用正切的二倍角公式求得tan=∠AOB,进而求得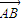 和
和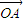 的关系令
的关系令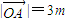 进而可表示出
进而可表示出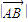 和
和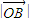 ,进而求得
,进而求得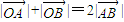 推断出
推断出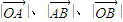 依次成等差数列.
依次成等差数列.
(II)由c,分别可求得a和b,进而求得双曲线的方程,设直线AB的斜率为k,进而利用tan∠BFX求得k,进而求得AB的方程,与双曲线方程联立,消去y,利用韦达定理表示出x1+x2和x1x2,进而根据弦长公式求得CD.
解答:解:(I)由已知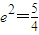 ,即
,即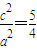 ,故
,故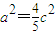 ①
①
从而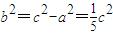 ②,
②,
故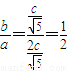
设∠AOF=∠BOF=θ,则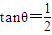
故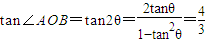 ,
,
即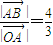 令
令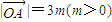 ,则
,则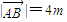 ,
,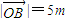 ,
,
满足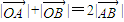 ,
,
所以,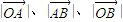 依次成等差数列
依次成等差数列
(II)由已知c2=5,代入①,②得a2=4,b2=1,
于是双曲线的方程为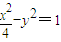
设直线AB的斜率为k,则k=tan∠BFX=tan∠AFO=cotθ=2
于是直线AB的方程为: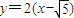
联立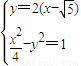 ,消y得
,消y得
故弦CD的长度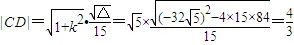
点评:本题主要考查了直线与圆锥曲线的综合问题,双曲线的标准方程,双曲线的性质.考查了学生对圆锥曲线基础知识的掌握和灵活运用.
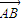 和
和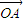 的关系令
的关系令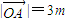 进而可表示出
进而可表示出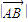 和
和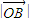 ,进而求得
,进而求得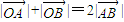 推断出
推断出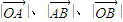 依次成等差数列.
依次成等差数列.(II)由c,分别可求得a和b,进而求得双曲线的方程,设直线AB的斜率为k,进而利用tan∠BFX求得k,进而求得AB的方程,与双曲线方程联立,消去y,利用韦达定理表示出x1+x2和x1x2,进而根据弦长公式求得CD.
解答:解:(I)由已知
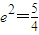 ,即
,即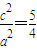 ,故
,故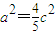 ①
①从而
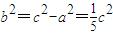 ②,
②,故
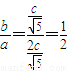
设∠AOF=∠BOF=θ,则
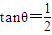
故
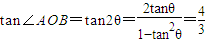 ,
,即
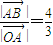 令
令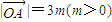 ,则
,则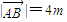 ,
,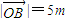 ,
,满足
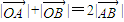 ,
,所以,
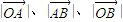 依次成等差数列
依次成等差数列(II)由已知c2=5,代入①,②得a2=4,b2=1,
于是双曲线的方程为
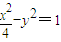
设直线AB的斜率为k,则k=tan∠BFX=tan∠AFO=cotθ=2
于是直线AB的方程为:
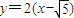
联立
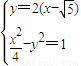 ,消y得
,消y得
故弦CD的长度
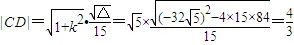
点评:本题主要考查了直线与圆锥曲线的综合问题,双曲线的标准方程,双曲线的性质.考查了学生对圆锥曲线基础知识的掌握和灵活运用.

练习册系列答案
相关题目
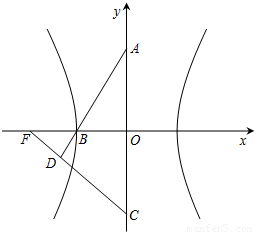
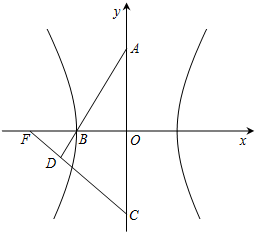 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是( )
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是( )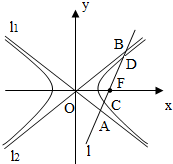 如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率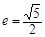 .
.
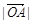 ,
,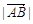 ,
,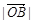 依次成等差数列;
依次成等差数列;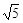 ,0),求直线AB在双曲线上所截得的弦CD的长度.
,0),求直线AB在双曲线上所截得的弦CD的长度.