题目内容
已知P(x,y)是函数y=ex+x图象上的点,则点P到直线2x-y-3=0的最小距离为
.
| 4 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
分析:求出平行于直线2x-y-3=0的曲线的切线,切点坐标,在乎利用点到直线的距离公式,即可求得结论.
解答:解:直线2x-y-3=0的斜率为2
求导函数可得y′=ex+1,令ex+1=2,则x=0,此时y=1,
即平行于直线2x-y-3=0的曲线的切线,切点坐标为(0,1)
∴点P到直线2x-y-3=0的最小距离为
=
故答案为:
求导函数可得y′=ex+1,令ex+1=2,则x=0,此时y=1,
即平行于直线2x-y-3=0的曲线的切线,切点坐标为(0,1)
∴点P到直线2x-y-3=0的最小距离为
| |0-1-3| | ||
|
| 4 |
| 5 |
| 5 |
故答案为:
| 4 |
| 5 |
| 5 |
点评:本题考查导数知识的运用,考查导数的几何意义,考查学生的计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知y=Asin(ωx+?)的最大值为1,在区间[
已知y=Asin(ωx+?)的最大值为1,在区间[| π |
| 6 |
| 2π |
| 3 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、以上都不是 |
 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )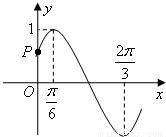



 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )



 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )



 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )


