题目内容
已知数列{an}的首项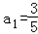 ,
,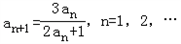 .
.
(1)求证:数列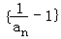 为等比数列;
为等比数列;
(2)记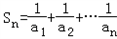 ,若Sn<100,求最大的正整数n.
,若Sn<100,求最大的正整数n.
(3)是否存在互不相等的正整数m,s,n,使m,s,n成等差数列且am﹣1,as﹣1,an﹣1成等比数列,如果存在,请给出证明;如果不存在,请说明理由.
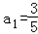 ,
,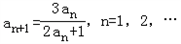 .
.(1)求证:数列
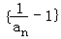 为等比数列;
为等比数列;(2)记
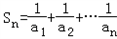 ,若Sn<100,求最大的正整数n.
,若Sn<100,求最大的正整数n.(3)是否存在互不相等的正整数m,s,n,使m,s,n成等差数列且am﹣1,as﹣1,an﹣1成等比数列,如果存在,请给出证明;如果不存在,请说明理由.
解:(1)∵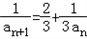 ,
,
∴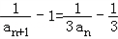 ,
,
∵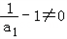 ,
,
∴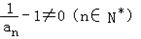 ,
,
∴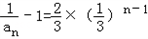 ,
,
∴数列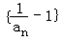 为等比数列.
为等比数列.
(2)由(1)可求得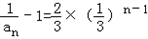 ,
,
∴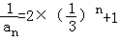 .
.
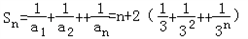 =
=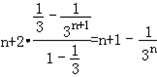 ,
,
若Sn<100,则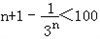 ,
,
∴nmax=99.
(3)假设存在,则m+n=2s,(am﹣1)●(an﹣1)=(as﹣1)2,
∵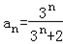 ,
,
∴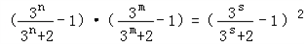 .
.
化简得:3m+3n=2●3s,
∵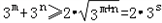 ,当且仅当m=n时等号成立.
,当且仅当m=n时等号成立.
又m,n,s互不相等,
∴不存在.
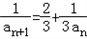 ,
,∴
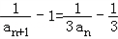 ,
,∵
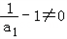 ,
,∴
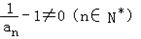 ,
,∴
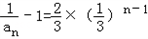 ,
,∴数列
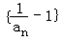 为等比数列.
为等比数列.(2)由(1)可求得
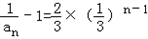 ,
,∴
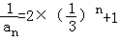 .
.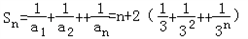 =
=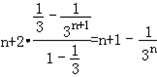 ,
,若Sn<100,则
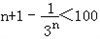 ,
,∴nmax=99.
(3)假设存在,则m+n=2s,(am﹣1)●(an﹣1)=(as﹣1)2,
∵
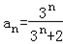 ,
,∴
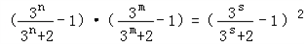 .
.化简得:3m+3n=2●3s,
∵
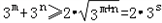 ,当且仅当m=n时等号成立.
,当且仅当m=n时等号成立.又m,n,s互不相等,
∴不存在.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目