题目内容
设命题p:(4x-3)2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,若 p是
p是 q的必要不充分条件,求实数a的取值范围.
q的必要不充分条件,求实数a的取值范围.
解 设A={x|(4x-3)2≤1},B={x|x2-(2a+1)x+a(a+1)≤0},易知
A={x| ≤x≤1},B={x|a≤x≤a+1}.
≤x≤1},B={x|a≤x≤a+1}.
由 p是
p是 q的必要不充分条件,从而p是q的充分不必要条件,即A
q的必要不充分条件,从而p是q的充分不必要条件,即A B,∴
B,∴
故所求实数a的取值范围是[0, ].
].

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 的两条渐近线分别为
的两条渐近线分别为 ,右焦点为
,右焦点为 ,若在右支上存在一点
,若在右支上存在一点 ,使得
,使得 的距离
的距离 、
、 、
、 的距离
的距离 依次成等比数列,则该双曲线的离心率
依次成等比数列,则该双曲线的离心率 的取值范围是( )
的取值范围是( ) B、
B、 C、
C、 D、
D、
 为一条直线,
为一条直线, ,
, ,
, 为三个互不重合的平面,给出下面三个命题:
为三个互不重合的平面,给出下面三个命题: ,
, //
// ,
, ,则
,则 ;
; ,则
,则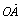 +
+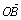 +
+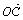 ,向量b=
,向量b=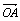 B.
B.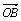 C.
C. ,则函数
,则函数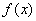 的值域是( ).
的值域是( ).  B.
B. C.
C. D.
D.
 ,符号
,符号 表示不超过
表示不超过 的最大整数,若关于
的最大整数,若关于 (
( 为常数)有且仅有3个不等的实根,则
为常数)有且仅有3个不等的实根,则 B.
B. 
 D.
D.
 的单调递增区间是( )
的单调递增区间是( ) B.
B. C.
C. D.
D.
 则不等式
则不等式 的解集是 ( )
的解集是 ( ) B.
B.
 D.
D.