题目内容
函数 的定义域________.
的定义域________.
(2k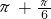 ,2k
,2k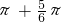 )(k∈Z)
)(k∈Z)
分析:函数y=log2x的定义域为{x|x>0},结合sinx∈[-1,1]及正弦函数的单调性、周期性可求得复合函数函数定义域.
解答:函数 由y=log2u和
由y=log2u和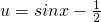 复合而成,
复合而成,
函数y=log2x的定义域为{x|x>0},所以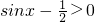 ,
,
又∵sinx∈[-1,1],是周期函数,最小正周期为2π,
∴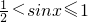 ,解得x∈(
,解得x∈(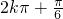 ,
,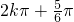 ),(k∈Z)
),(k∈Z)
故答案为(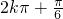 ,
,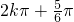 ),(k∈Z).
),(k∈Z).
点评:本题考查复合函数的定义域的求解,以此为平台,求解正弦函数不等式,熟练掌握正弦函数的周期性、单调性及值域才能正确解题,这些性质应结合函数图形掌握,本题属于中档题.
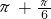 ,2k
,2k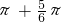 )(k∈Z)
)(k∈Z)分析:函数y=log2x的定义域为{x|x>0},结合sinx∈[-1,1]及正弦函数的单调性、周期性可求得复合函数函数定义域.
解答:函数
 由y=log2u和
由y=log2u和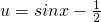 复合而成,
复合而成,函数y=log2x的定义域为{x|x>0},所以
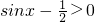 ,
,又∵sinx∈[-1,1],是周期函数,最小正周期为2π,
∴
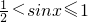 ,解得x∈(
,解得x∈(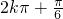 ,
,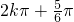 ),(k∈Z)
),(k∈Z)故答案为(
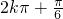 ,
,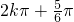 ),(k∈Z).
),(k∈Z).点评:本题考查复合函数的定义域的求解,以此为平台,求解正弦函数不等式,熟练掌握正弦函数的周期性、单调性及值域才能正确解题,这些性质应结合函数图形掌握,本题属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.写出y关于x的函数关系式,并指出这个函数的定义域.
如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.写出y关于x的函数关系式,并指出这个函数的定义域.