题目内容
.已知![]() ,且
,且![]() .
.
(1)求sinx、cosx、tanx的值.
(2)求sin3x – cos3x的值.
(1)![]()
![]()
![]() (2) sin3x – cos3x= 91/125
(2) sin3x – cos3x= 91/125
解析:
(1)由![]() ,得
,得![]()
代入sin2x+cos2x=1得:(5cosx-4)(5cosx+3)=0
∴![]() 或
或![]()
当![]() 时,得
时,得![]()
又∵![]() ,∴sinx>0,故这组解舍去
,∴sinx>0,故这组解舍去
当![]() 时,
时,![]() ,
,![]()
(2)∵![]()
∴(sinx+cosx)2 = sin2x+cos2x+2sinxcosx =![]()
∴![]()
又![]() ,sinx>0,∴cosx<0
,sinx>0,∴cosx<0
(sinx-cosx)2=1-2sinxcosx=![]()
又∵sinx – cosx>0∴sinx – cosx =![]()
sin3x – cos3x = (sinx-cosx)(sin2x+sinxcosx+cos2x)=![]()

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
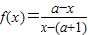 ,且f-1(x-1)的图象的对称中心是(0,3),则a的值为( )
,且f-1(x-1)的图象的对称中心是(0,3),则a的值为( )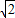
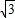
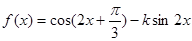 ,且
,且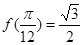 .
.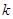 的值;
的值;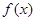 的单调递增区间及最大值,并指出取得最大值时的
的单调递增区间及最大值,并指出取得最大值时的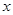 值.
值.  ,
, 且
且
 的周期;
的周期;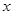 的值;
的值; ,且
,且
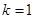 ,求
,求 ;
;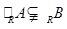 ,求实数
,求实数 的取值范围.
的取值范围.