题目内容
用数学归纳法证明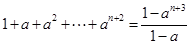 (
(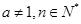 ),在验证当n=1时,等式左边应为
),在验证当n=1时,等式左边应为
| A.1 | B.1+a | C.1+a+a2 | D.1+a+a2+a3 |
D
解析试题分析:注意到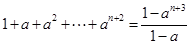 的左端,表示
的左端,表示 直到
直到 共n+3项的和,所以,当n=1时,等式左边应为1+a+a2+a3,选D。
共n+3项的和,所以,当n=1时,等式左边应为1+a+a2+a3,选D。
考点:数学归纳法
点评:简单题,应用数学归纳法证明问题,应遵循“两步一结”。对于,n=1的情况,注意明确“项数”。

练习册系列答案
相关题目
下面使用类比推理正确的是( )
A.“若 ,则 ,则 ”类推出“若 ”类推出“若 ,则 ,则 ” ” |
B.“若 ”类推出“ ”类推出“ ” ” |
C.“若 ”类推出“ ”类推出“ ( ( )” )” |
D.“ ” 类推出“ ” 类推出“ ” ” |
将 个正整数
个正整数 、
、 、
、 、…、
、…、 (
( )任意排成
)任意排成 行
行 列的数表.对于某一个数表,计算各行和各列中的任意两个数
列的数表.对于某一个数表,计算各行和各列中的任意两个数 、
、 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.当
,称这些比值中的最小值为这个数表的“特征值”.当 时,数表的所有可能的“特征值”最大值为
时,数表的所有可能的“特征值”最大值为
A. | B. | C. | D. |
用反证法证明命题:“已知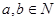 ,若
,若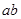 可被5整除,则
可被5整除,则 中至少有一个能被5整除”时,反设正确的是( )
中至少有一个能被5整除”时,反设正确的是( )
A. 都不能被5整除 都不能被5整除 | B. 都能被5整除 都能被5整除 |
C. 中有一个不能被5整除 中有一个不能被5整除 | D. 中有一个能被5整除 中有一个能被5整除 |
在集合{a,b,c,d}上定义两种运算⊕和?如下:
那么d?(a⊕c)等于( )
| A.a | B.b | C.c | D.d |
有一段演绎推理是这样的:“若直线平行于平面,则该直线平行于平面内所有直线;已知直线b∥平面α,直线a?平面α,则直线b∥直线a”,结论显然是错误的,这是因为( )
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |
推理“①矩形是平行四边形;②正方形是矩形;③正方形是平行四边形”中的小前提是( )
| A.① | B.② |
| C.③ | D.以上均错 |
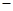 LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 .
LMN,如果用S1,S2,S3表示三个侧面面积,S4表示截面面积,那么你类比得到的结论是 . 

 则
则 ______;
______;