题目内容
等差数列{an}中,前n项和Sn= ,前m项和Sm=
,前m项和Sm= (m≠n),则Sm+n
(m≠n),则Sm+n
- A.小于4
- B.等于4
- C.大于4
- D.大于2且小于4
C
分析:分别利用等差数列的前n项和的公式表示出Sn,Sm及Sm+n,然后将Sn= 和Sm=
和Sm= 的值代入Sm+n,化简后,根据m,n为正整数且m不等于n,取最小m=1,n=2,求出此时公差d的值,即可得到Sm+n的最小值,求出的最小值大于4,得到正确答案.
的值代入Sm+n,化简后,根据m,n为正整数且m不等于n,取最小m=1,n=2,求出此时公差d的值,即可得到Sm+n的最小值,求出的最小值大于4,得到正确答案.
解答:设等差数列的公差为d,
则Sn= =
=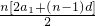 =
= ,
,
同理Sm=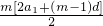 =
= ,
,
则Sm+n=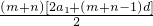 =
=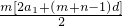 +
+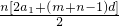
=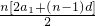 +
+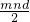 +
+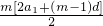 +
+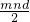
= +
+ +mnd,
+mnd,
因为m,n为正整数,且m≠n,令n>m,m=1,n=2,
将m=1,n=2代入Sn中得到2a1+d=2;代入Sm中得到a1= ,
,
解得d=1,
则Sm+n≥2+ +2=
+2= >4.
>4.
故选C
点评:此题考查学生灵活运用等差数列的前n项和的公式化简求值,是一道中档题.
分析:分别利用等差数列的前n项和的公式表示出Sn,Sm及Sm+n,然后将Sn=
 和Sm=
和Sm= 的值代入Sm+n,化简后,根据m,n为正整数且m不等于n,取最小m=1,n=2,求出此时公差d的值,即可得到Sm+n的最小值,求出的最小值大于4,得到正确答案.
的值代入Sm+n,化简后,根据m,n为正整数且m不等于n,取最小m=1,n=2,求出此时公差d的值,即可得到Sm+n的最小值,求出的最小值大于4,得到正确答案.解答:设等差数列的公差为d,
则Sn=
 =
=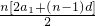 =
= ,
,同理Sm=
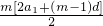 =
= ,
,则Sm+n=
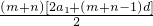 =
=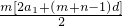 +
+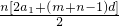
=
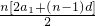 +
+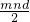 +
+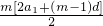 +
+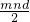
=
 +
+ +mnd,
+mnd,因为m,n为正整数,且m≠n,令n>m,m=1,n=2,
将m=1,n=2代入Sn中得到2a1+d=2;代入Sm中得到a1=
 ,
,解得d=1,
则Sm+n≥2+
 +2=
+2= >4.
>4.故选C
点评:此题考查学生灵活运用等差数列的前n项和的公式化简求值,是一道中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目