题目内容
对命题p:“1是集合{x|x2<a}中的元素”,q:“2是集合{x|x2<a}中的元素”,则a为何值时,“p或q”是真命题?a为何值时,“p且q”是真命题?
解:因为1是集合{x|x2<a}中的元素,所以有a>1;又因为2是集合{x|x2<a}中的元素,所以a>4.
由于“p或q”是真命题,所以有{a|a>1}∪{a|a>4}={a|a>1},即当a>1时,“p或q”是真命题.
由于“p且q”是真命题,所以有{a|a>1}∩{a|a>4}={a|a>4},即当a>4时,“p且q”是真命题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
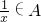 .则称集合A是“好集”.
.则称集合A是“好集”. .
.