题目内容
椭圆E: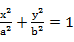 (a>b>0)的焦点到直线x-3y=0的距离为
(a>b>0)的焦点到直线x-3y=0的距离为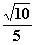 ,离心率为
,离心率为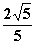 ;抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点,与E交于A,B,与G交于C,D.
;抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点,与E交于A,B,与G交于C,D.
(1)求椭圆E及抛物线G的方程;
(2)是否存在常数λ,使 为常数,若存在,求出λ的值,若不存在,请说明理由.
为常数,若存在,求出λ的值,若不存在,请说明理由.
[解析](1)当 时,
时, ,(1分)
,(1分)
当 时,
时, (2分)
(2分)
而当 时,
时, , ∴
, ∴ (
( ). (4分)
). (4分)
(2) ,
,
∴ .(7分)
.(7分)
∵ ,
,
∴ 单调递增,
单调递增, . (8分)
. (8分)
令 ,得
,得 ,所以
,所以 . (10分)
. (10分)
(3)
当 为奇数时,
为奇数时, 为偶数,∴
为偶数,∴ ,
, . (12分)
. (12分)
当 为偶数时,
为偶数时, 为奇数,∴
为奇数,∴ ,
, (舍去)
(舍去)
综上,存在唯一正整数 ,使得
,使得 成立. (14分)
成立. (14分)

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
某学生对一些对数进行运算,如下图表格所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是 ( )
A.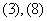 B.
B.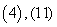 C.
C.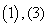 D.
D.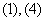






 (1)
(1) (2)
(2) (3)
(3) (4)
(4)



 (5)
(5) (6)
(6) (7)
(7) (8)
(8)


 (9)
(9) (10)
(10) (11)
(11)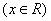 满足f(
满足f(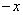 )=f(x),f(x)=f(2
)=f(x),f(x)=f(2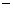 x),且当
x),且当 时,f(x)=x3.又函数g(x)=|xcos
时,f(x)=x3.又函数g(x)=|xcos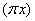 |,则函数h(x)=g(x)-f(x)在
|,则函数h(x)=g(x)-f(x)在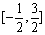 上的零点个数为
上的零点个数为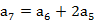 ,若存在两项
,若存在两项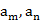 ,使得
,使得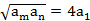 ,则
,则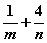 的最小值为( )
的最小值为( ) B.
B. C.
C. D.不存在
D.不存在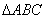 的边
的边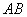 、
、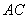 上分别取
上分别取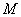 、
、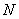 ,使
,使 ,
, ,
,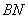 与
与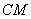 交于点
交于点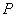 ,若
,若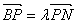 ,
,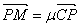 ,则
,则 .
.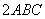 =S△BCM·S△BCD.上述命题是( )
=S△BCM·S△BCD.上述命题是( )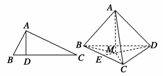
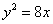 的焦点与双曲线
的焦点与双曲线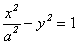 的一个焦点重合,则该双曲线
的一个焦点重合,则该双曲线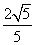 B.
B.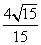 C.
C.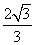 D.
D.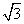
 满足
满足 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.