题目内容
【题目】已知点A（1，﹣1），B（4，0），C（2，2），平面区域D是所有满足 
= 
+μ 
（1＜λ≤a，1＜μ≤b）的点P（x，y）组成的区域．若区域D的面积为8，则4a+b的最小值为 （ ）
A.5
B.4 
C.9
D.5+4
【答案】C
【解析】解：如图所示，
延长AB到点N，延长AC到点M，使得|AN|=a|AB|，|AM|=b|AC|，作CH∥AN，BF∥AM，NG∥AM，MG∥AN，则四边形ABEC，ANGM，EHGF均为平行四边形．由题意可知：点P（x，y）组成的区域D为图中的四边形EFGH及其内部．
∵ 
=（3，1）， 
=（1，3）， 
=（﹣2，2），∴ 
= 
， 
= ， 
=2 
．
∴cos∠CAB=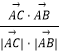 
= 
= 
， 
．
∴四边形EFGH的面积S= 
=8，
∴（a﹣1）（b﹣1）=1，即 
．
∴4a+b=（4a+b） 
=5+ 
=9，当且仅当b=2a=3时取等号．
∴4a+b的最小值为9．
故选：C．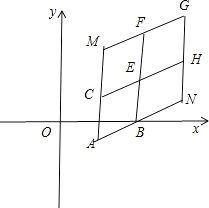
【考点精析】解答此题的关键在于理解基本不等式的相关知识，掌握基本不等式：
,（当且仅当
时取到等号）；变形公式：
，以及对平面向量的基本定理及其意义的理解，了解如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
．
练习册系列答案
相关题目
