题目内容
【题目】当x∈[0，1]时，下列关于函数y=
的图象与
的图象交点个数说法正确的是（ ）
A. 当
时，有两个交点B. 当
时，没有交点
C. 当
时，有且只有一个交点D. 当
时，有两个交点
【答案】B
【解析】
结合函数图象、二次函数性质，分类讨论判断选择项真假.
设f（x）=
，g（x）=
，其中x∈[0，1]
A．若m=0，则
与
在[0，1]上只有一个交点
，故A错误．
B．当m∈（1，2）时，
即当m∈（1，2]时，函数y=的图象与
的图象在x∈[0，1]无交点，故B正确，
C．当m∈（2，3]时，
，
当
时
，此时无交点，即C不一定正确．
D．当m∈（3，+∞）时，g（0）=
＞1，此时f（1）＞g（1），此时两个函数图象只有一个交点，故D错误，
故选：B．
中考解读考点精练系列答案
【题目】为了调查高中生的数学成绩与学生自主学习时间之间的相关关系，新苗中学数学教师对新入学的
名学生进行了跟踪调查，其中每周自主做数学题的时间不少于
小时的有
人，余下的人中，在高三模拟考试中数学成绩不足
分的占
，统计成绩后，得到如下的
列联表：
分数大于等于 | 分数不足 | 合计 | |
周做题时间不少于 | 4 | 19 | |
周做题时间不足 | |||
合计 | 45 |
（
）请完成上面的列联表，并判断能否在犯错误的概率不超过
的前提下认为“高中生的数学成绩与学生自主学习时间有关”．
（
）（i）按照分层抽样的方法，在上述样本中，从分数大于等于
分和分数不足分的两组学生中抽取
名学生，设抽到的不足分且周做题时间不足小时的人数为
，求的分布列（概率用组合数算式表示）．
（ii）若将频率视为概率，从全校大于等于分的学生中随机抽取
人，求这些人中周做题时间不少于小时的人数的期望和方差．
附：
|
|
|
|
|
|
|
|
【题目】已知某单位全体员工年龄频率分布表为：
年龄（岁） | [25，30） | [30，35） | [35，40） | [40，45） | [45，50） | [50，55） | 合计 |
人数（人） | 6 | 18 | 50 | 31 | 19 | 16 | 140 |
经统计，该单位35岁以下的青年职工中，男职工和女职工人数相等，且男职工的年龄频率分布直方图和如图所示：
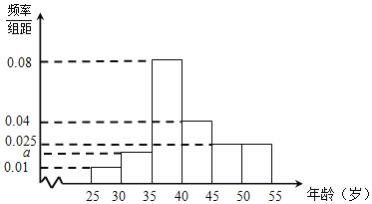
（Ⅰ）求a；
（Ⅱ）求该单位男女职工的比例；
（Ⅲ）若从年龄在[25，30）岁的职工中随机抽取两人参加某项活动，求恰好抽取一名男职工和一名女职工的概率．
