题目内容
(本小题满分12分)
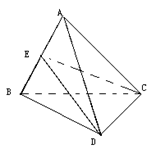
如图,已知空间四边形ABCD中,BC=AC, AD=BD,E是AB的中点,
AD=BD,E是AB的中点,
求证:
AB⊥平面CDE;
平面CDE⊥平面ABC;
若G为△ADC的重心,试在线段AB上确定一点F,使得GF∥平面CDE.
如图,已知空间四边形ABCD中,BC=AC,
 AD=BD,E是AB的中点,
AD=BD,E是AB的中点,
求证:
AB⊥平面CDE;
平面CDE⊥平面ABC;
若G为△ADC的重心,试在线段AB上确定一点F,使得GF∥平面CDE.
(1)证明略
(2)证明略
(3)略
解:(1)证明:
同理
又 -----------5分
-----------5分
(2)证明:由(1)知 平面CDE
平面CDE
又 平面ABC,
平面ABC, 平面CDE
平面CDE 平面ABC -------7分
平面ABC -------7分
(3)解:连接AG,并延长交CD于H,连接EH,则
在AB上取点F,使得 ,则GF//EH,
,则GF//EH,
易知GF//平面CDE ---------12分

同理

又
 -----------5分
-----------5分(2)证明:由(1)知
 平面CDE
平面CDE又
 平面ABC,
平面ABC, 平面CDE
平面CDE 平面ABC -------7分
平面ABC -------7分(3)解:连接AG,并延长交CD于H,连接EH,则

在AB上取点F,使得
 ,则GF//EH,
,则GF//EH,易知GF//平面CDE ---------12分

练习册系列答案
相关题目

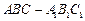 中,
中,  底面
底面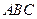 ,
,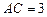 ,
, 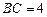 ,
,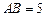 , 点D是
, 点D是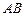 的中点.
的中点.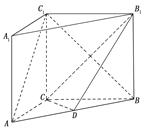
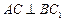 ; (Ⅱ) 求证
; (Ⅱ) 求证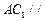 ∥平面
∥平面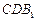 .
.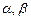 为两个不重合的平面,
为两个不重合的平面,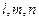 为两两不重合的直线,给出下列四个命题:①若
为两两不重合的直线,给出下列四个命题:①若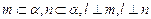 ,则
,则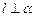 ;②若
;②若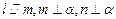 ,则
,则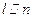 ;③若
;③若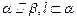 ,则
,则 ;④若
;④若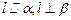 ,则
,则 .其中正确命题的序号是 ▲ .
.其中正确命题的序号是 ▲ .
 和平面
和平面 ,且
,且 ,那么( )
,那么( )
 不在
不在 内
内


 为平面,
为平面, 为直线,则
为直线,则 的一个充分条件是 ( )
的一个充分条件是 ( )



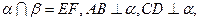 垂足分别是B、D,如果增加一个条件,就能推出
垂足分别是B、D,如果增加一个条件,就能推出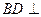 EF,这个条件不可能是下面四个选项中的( )
EF,这个条件不可能是下面四个选项中的( )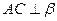
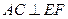
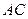 与a、b所成的角相等
与a、b所成的角相等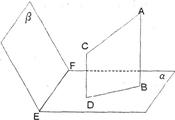
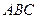
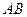
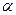
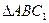 是( )
是( )