题目内容
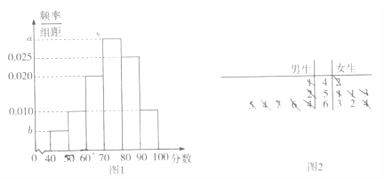
【题目】某教育主管部门到一所中学检查高三年级学生的体质健康情况，从中抽取了
名学生的体质测试成绩，得到的频率分布直方图如图1所示，样本中前三组学生的原始成绩按性别分类所得的茎叶图如图2所示.
（Ⅰ）求
， 
， 
的值；
（Ⅱ）估计该校高三学生体质测试成绩的平均数
和中位数
；
（Ⅲ）若从成绩在
的学生中随机抽取两人重新进行测试，求至少有一名男生的概率.
【答案】（Ⅰ）
.
（Ⅱ）
.
（Ⅲ）
.
【解析】试题分析：（Ⅰ）由茎叶图可知分数在
的有
人，进而求解
的值；
（Ⅱ）根据数据平均数的计算公式，即可求得
的值．
（Ⅲ）两名男生分别记为
， 
，四名女生分别记为
， 
， 
， 
，列举出从中任取两人的基本事件的总数，即可利用古典概率的概率计算公式求解概率．
试题解析：
（Ⅰ）由茎叶图可知分数在
的有4人，
所以
， 
， 
，
解得
.
（Ⅱ）
，
由
，得
.
（Ⅲ）两名男生分别记为
， 
，四名女生分别记为
， 
， 
， 
，
从中任取两人共有
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共15种结果，至少有一名男生的结果有
， 
， 
， 
， 
， 
， 
， 
， 
，共9种结果，所以至少有一名男生的概率为
.
【题目】为了适应高考改革，某中学推行“创新课堂”教学．高一平行甲班采用“传统教学”的教学方式授课，高一平行乙班采用“创新课堂”的教学方式授课，为了比较教学效果，期中考试后，分别从两个班中各随机抽取
名学生的成绩进行统计分析，结果如下表：（记成绩不低于
分者为“成绩优秀”）
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
（Ⅰ）由以上统计数据填写下面的
列联表，并判断是否有
以上的把握认为“成绩优秀与教学方式有关”？
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
（Ⅱ）现从上述样本“成绩不优秀”的学生中，抽取
人进行考核，记“成绩不优秀”的乙班人数为
，求的分布列和期望．
参考公式：
，其中
．
临界值表
|
|
|
|
|
|
|
|
|
|
