题目内容
已知函数 ,直线
,直线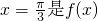 象的一条对称轴.
象的一条对称轴.
(1)试求ω的值:
(2)若函数y=g(x)的图象是由y=f(x)图象上的各点的横坐标伸长到原来的2倍,然后再向左平移 个单位长度得到,求函数g(x)在[0,
个单位长度得到,求函数g(x)在[0, ]上的最大值.
]上的最大值.
解: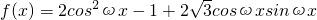 =cos2ωx+
=cos2ωx+ sin2ωx=2sin(2ωx+
sin2ωx=2sin(2ωx+ ),
),
(1)∵直线 是f(x)图象的一条对称轴
是f(x)图象的一条对称轴
∴ 是方程2ωx+
是方程2ωx+ =kπ+
=kπ+ (k∈Z)的一个解,
(k∈Z)的一个解,
即2ω• +
+ =kπ+
=kπ+ ,得ω=
,得ω= (3k+1)
(3k+1)
∵0<ω<1,取k=0,得ω= ;
;
(2)y=f(x)图象上的各点的横坐标伸长到原来的2倍,得到y=f( )的图象
)的图象
再将所得图象向左平移 个单位长度,得到y=f(
个单位长度,得到y=f(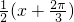 )的图象,
)的图象,
∴g(x)=f(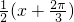 )=2sin[2•
)=2sin[2• •
•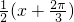 +
+ ]=2sin(
]=2sin( +
+ )=2cos
)=2cos ,
,
∵0≤x≤ ,∴0≤
,∴0≤ ≤
≤ ,可得
,可得 ≤cos
≤cos ≤1
≤1
由此可得g(x)∈[ ,2],在[0,
,2],在[0, ]上的最大值为2.
]上的最大值为2.
分析:(1)将函数f(x)利用二倍角余弦公式和辅助角公式化简,得f(x)=2sin(2ωx+ ),根据正弦函数对称轴方程的结论得
),根据正弦函数对称轴方程的结论得 是方程2ωx+
是方程2ωx+ =kπ+
=kπ+ (k∈Z)的一个解,建立关于ω的方程,结合0<ω<1可得ω的值;
(k∈Z)的一个解,建立关于ω的方程,结合0<ω<1可得ω的值;
(2)根据三角函数图象变换的公式,得到g(x)=f(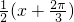 ),化简得g(x)=2cos
),化简得g(x)=2cos ,结合余弦函数的图象,不难得到g(x)在[0,
,结合余弦函数的图象,不难得到g(x)在[0, ]上的最大值.
]上的最大值.
点评:本题给出含有字母参数的三角函数表达式,在已知一条对称轴的情况下求参数的值,并求函数图象变换后所得函数的最大值,着重考查了正弦函数的对称性、三角函数中的恒等变换应用和函数y=Asin(ωx+φ)的图象变换等知识,属于中档题.
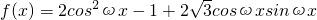 =cos2ωx+
=cos2ωx+ sin2ωx=2sin(2ωx+
sin2ωx=2sin(2ωx+ ),
),(1)∵直线
 是f(x)图象的一条对称轴
是f(x)图象的一条对称轴∴
 是方程2ωx+
是方程2ωx+ =kπ+
=kπ+ (k∈Z)的一个解,
(k∈Z)的一个解,即2ω•
 +
+ =kπ+
=kπ+ ,得ω=
,得ω= (3k+1)
(3k+1)∵0<ω<1,取k=0,得ω=
 ;
;(2)y=f(x)图象上的各点的横坐标伸长到原来的2倍,得到y=f(
 )的图象
)的图象再将所得图象向左平移
 个单位长度,得到y=f(
个单位长度,得到y=f(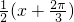 )的图象,
)的图象,∴g(x)=f(
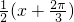 )=2sin[2•
)=2sin[2• •
•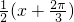 +
+ ]=2sin(
]=2sin( +
+ )=2cos
)=2cos ,
,∵0≤x≤
 ,∴0≤
,∴0≤ ≤
≤ ,可得
,可得 ≤cos
≤cos ≤1
≤1由此可得g(x)∈[
 ,2],在[0,
,2],在[0, ]上的最大值为2.
]上的最大值为2.分析:(1)将函数f(x)利用二倍角余弦公式和辅助角公式化简,得f(x)=2sin(2ωx+
 ),根据正弦函数对称轴方程的结论得
),根据正弦函数对称轴方程的结论得 是方程2ωx+
是方程2ωx+ =kπ+
=kπ+ (k∈Z)的一个解,建立关于ω的方程,结合0<ω<1可得ω的值;
(k∈Z)的一个解,建立关于ω的方程,结合0<ω<1可得ω的值;(2)根据三角函数图象变换的公式,得到g(x)=f(
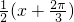 ),化简得g(x)=2cos
),化简得g(x)=2cos ,结合余弦函数的图象,不难得到g(x)在[0,
,结合余弦函数的图象,不难得到g(x)在[0, ]上的最大值.
]上的最大值.点评:本题给出含有字母参数的三角函数表达式,在已知一条对称轴的情况下求参数的值,并求函数图象变换后所得函数的最大值,着重考查了正弦函数的对称性、三角函数中的恒等变换应用和函数y=Asin(ωx+φ)的图象变换等知识,属于中档题.

练习册系列答案
相关题目
 ,直线
,直线 图象的一条对称轴.
图象的一条对称轴. 个单位长度得到,若
个单位长度得到,若 的值.
的值.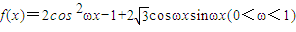 ,直线
,直线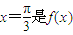 象的一条对称轴.
象的一条对称轴.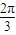 个单位长度得到,求函数g(x)在[0,
个单位长度得到,求函数g(x)在[0,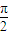 ]上的最大值.
]上的最大值.