题目内容
18.已知0≤x≤1时,不等式-4x2+4ax-4a-a2≤-5恒成立,求实数a的取值范围.分析 构造函数f(x)=-4x2+4ax-4a-a2+5.x∈[0,1].
分类讨论(1)当△≤0时,即a$≤-\frac{5}{4}$,f(x)≤0恒成立,
(2)当△>0时,即a$>-\frac{5}{4}$,利用对称轴的位置得出不等式组只需$\left\{\begin{array}{l}{\frac{a}{2}≥1}\\{f(1)=-4+4a-4a-{a}^{2}+5≤0}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{a}{2}≤0}\\{f(0)=-4a-{a}^{2}+5≤0}\end{array}\right.$求解即可.
解答 解:设函数f(x)=-4x2+4ax-4a-a2+5.x∈[0,1].
对称轴x=$\frac{a}{2}$,△=16a2-4×(-4)×(-4a-a2+5)=64a+80,
(1)当△≤0时,即a$≤-\frac{5}{4}$,f(x)≤0恒成立,
即0≤x≤1时,不等式-4x2+4ax-4a-a2≤-5恒成立,
(2)当△>0时,即a$>-\frac{5}{4}$,
要使0≤x≤1时,不等式-4x2+4ax-4a-a2≤-5恒成立,
只需$\left\{\begin{array}{l}{\frac{a}{2}≥1}\\{f(1)=-4+4a-4a-{a}^{2}+5≤0}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{a}{2}≤0}\\{f(0)=-4a-{a}^{2}+5≤0}\end{array}\right.$
求解得出$\left\{\begin{array}{l}{a≥2}\\{a≥1或a≤-1}\end{array}\right.$或$\left\{\begin{array}{l}{a≤0}\\{a≥1或a≤-5}\end{array}\right.$,
即可得出a≥2,使0≤x≤1时,不等式-4x2+4ax-4a-a2≤-5恒成立,
有(1)(2)得出a≥2或a$≤-\frac{5}{4}$.
故答案为:a≥2或a$≤-\frac{5}{4}$.
点评 本题综合考察了二次函数性质的运用求解函数最值与不等式恒成立问题的运用,关键分类讨论得出不等式组即可.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{4}{5}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{7}$ | D. | $\frac{1}{2}$ |
| A. | 两条直线 | B. | 两条双曲线 | ||
| C. | 两个点 | D. | 一条直线和一条双曲线 |
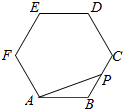 如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].
如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].