题目内容
设 到定点
到定点 的距离和它到直线
的距离和它到直线 距离的比是
距离的比是 .
.
(Ⅰ)求点 的轨迹方程;
的轨迹方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为 的直线过
的直线过 点,且与点
点,且与点 的轨迹交于点
的轨迹交于点 ,
, ,若
,若 ,求△
,求△ 的面积.
的面积.
(Ⅰ)  ;(Ⅱ)
;(Ⅱ) 
【解析】
试题分析:(Ⅰ)根据题意,由已知得 ,化简得点
,化简得点 的轨迹方程为
的轨迹方程为 ;(Ⅱ)设直线
;(Ⅱ)设直线 的方程为
的方程为 .联立方程组
.联立方程组 消元可得故
消元可得故 ,又
,又 ,所以
,所以 ,可得
,可得 ,所以
,所以 ,由
,由
原点 到直线
到直线 的距离
的距离 ,所以
,所以
试题解析:(Ⅰ)由已知得
化简得点 的轨迹方程为
的轨迹方程为 . 6分
. 6分
(Ⅱ)设直线 的方程为
的方程为 .联立方程组
.联立方程组
消去 并整理得
并整理得
故

又
所以 ,可得
,可得 ,所以
,所以
由
原点 到直线
到直线 的距离
的距离
所以 12分
12分
考点:轨迹方程及圆锥曲线定值问题
考点分析: 考点1:抛物线的标准方程 考点2:抛物线的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
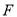 是抛物线
是抛物线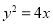 的焦点,点
的焦点,点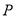 在该抛物线上,且点
在该抛物线上,且点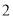 ,则
,则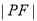 =( )
=( ) 的焦点坐标是( )
的焦点坐标是( ) B.
B. C.
C. D.
D.
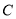 的两个焦点分别为
的两个焦点分别为 ,若曲线
,若曲线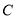 上存在点
上存在点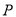 满足
满足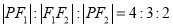 ,则曲线
,则曲线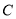 的离心率等于( )
的离心率等于( )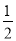 或
或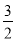 B.
B. 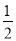 或
或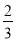 C.
C. 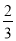
 是
是 的( )
的( ) 的最小值为 ☆
的最小值为 ☆  ,则( )
,则( )
 B.
B.
 D.
D.
 是定义在
是定义在 上的奇函数,在
上的奇函数,在 上单调递减,且
上单调递减,且 ,若
,若 ,则
,则 的取值范围为 .
的取值范围为 .
 ,BP=2,求QD.
,BP=2,求QD.