题目内容
在正△ABC中,E、F分别是AB、AC边上的点,满足将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B、A1C(如图(2)).
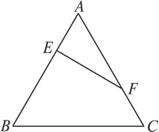
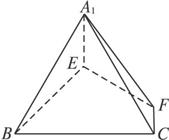
(1) (2)
(1)求证:A1E⊥平面BEC;
(2)求直线A1E与平面A1BC所成角的大小.
解:不妨设正△ABC的边长为3,则(1)在题图(1)中,取BE中点D,连结DF,
∵![]() =
=![]() =
=![]() ,
,
∴AE=1,AF=2.而∠A=60°,∴EF⊥AE.∵在题图(2)中有A1E⊥EF,BE⊥EF,
∴∠A1EB为二面角A1EFB的平面角.
∵二面角A1EFB为直二面角,∴A1E⊥BE.
又∵BE∩EF=E,∴A1E⊥平面BEC.
(2)过E作EH⊥BC于H,连结A1H,作EO⊥A1H于O,证明EO⊥平面A1BC,在Rt△A1EH中求得直线A1E与平面A1BP所成角的大小为![]() .
.

练习册系列答案
相关题目
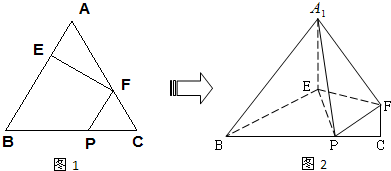

 ,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
 ,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
 ,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.