题目内容
在正△ABC中,E,F,P分别是AB,AC,BC边上的点,满足 ,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.(1)求证:A1E⊥平面BEP;
(2)求直线A1E与平面A1BP所成角的大小.

【答案】分析:(1)取BE的中点D,连接DF.说明∠A1EB为二面角A1-EF-B的平面角,证明二面角A1-EF-B为直二面角,证明A1E┴平面BEF,即可证明A1E⊥平面BEP;
(2)建立空间直角坐标系,求出 ,平面A1BP的法向量
,平面A1BP的法向量 ,利用
,利用 ,求直线A1E与平面A1BP所成角的大小.
,求直线A1E与平面A1BP所成角的大小.
解答:解:不妨设正三角形的边长为3.
(1)在图1中,取BE的中点D,连接DF.
∵ ,AF=AD=2,又∠A=60°,△ADF为正三角形.
,AF=AD=2,又∠A=60°,△ADF为正三角形.
又∵AE=ED=1,
∴EF┴AD,
∴在图2中有A1E┴EF,BE┴EF.
∴∠A1EB为二面角A1-EF-B的平面角.
∵二面角A1-EF-B为直二面角,
∴A1E┴BE
又∵BE∩EF=E,
∴即A1E┴平面BEF,即A1E┴平面BEP
(2)由(1)可知,A1E┴平面BEP,BE┴EF,建立坐标系则E(0,0,0),A1(0,0,1),(2,0,0),
F(0, ,0),D(1,0,0),不难得出EF∥DP且EF=DP,DE∥EP且DE=FP.
,0),D(1,0,0),不难得出EF∥DP且EF=DP,DE∥EP且DE=FP.
故P点的坐标为(1, ,0),
,0),
∴
设平面A1BP的法向量 =(x,y,z),
=(x,y,z),
则
∴ .
.
∴
∴A1E与平面A1BP所成角的大小为 .
.
点评:本题考查用空间向量求直线与平面的夹角,考查计算能力,空间想象能力,逻辑思维能力,是中档题.
(2)建立空间直角坐标系,求出
 ,平面A1BP的法向量
,平面A1BP的法向量 ,利用
,利用 ,求直线A1E与平面A1BP所成角的大小.
,求直线A1E与平面A1BP所成角的大小.解答:解:不妨设正三角形的边长为3.
(1)在图1中,取BE的中点D,连接DF.
∵
 ,AF=AD=2,又∠A=60°,△ADF为正三角形.
,AF=AD=2,又∠A=60°,△ADF为正三角形.又∵AE=ED=1,
∴EF┴AD,
∴在图2中有A1E┴EF,BE┴EF.
∴∠A1EB为二面角A1-EF-B的平面角.
∵二面角A1-EF-B为直二面角,
∴A1E┴BE
又∵BE∩EF=E,
∴即A1E┴平面BEF,即A1E┴平面BEP
(2)由(1)可知,A1E┴平面BEP,BE┴EF,建立坐标系则E(0,0,0),A1(0,0,1),(2,0,0),
F(0,
 ,0),D(1,0,0),不难得出EF∥DP且EF=DP,DE∥EP且DE=FP.
,0),D(1,0,0),不难得出EF∥DP且EF=DP,DE∥EP且DE=FP.故P点的坐标为(1,
 ,0),
,0),∴

设平面A1BP的法向量
 =(x,y,z),
=(x,y,z),则

∴
 .
.∴

∴A1E与平面A1BP所成角的大小为
 .
.点评:本题考查用空间向量求直线与平面的夹角,考查计算能力,空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
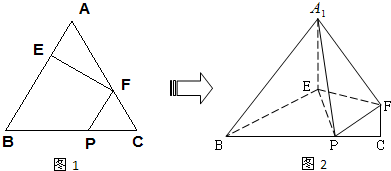

 ,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
 ,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.