题目内容
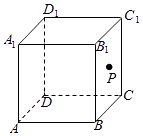
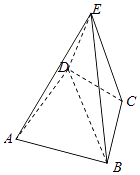
【题目】在矩形ABCD中,AB=4 ![]() ,AD=2
,AD=2 ![]() ,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.
,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.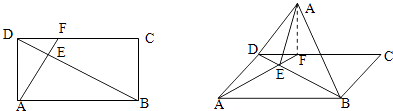
(1)当θ=90°时,求A′C的长;
(2)当cosθ= ![]() 时,求BC与平面A′BD所成角的正弦值.
时,求BC与平面A′BD所成角的正弦值.
【答案】
(1)解:在图1中,过A作BD的垂线交BD于E,交DC于F,连接CE.
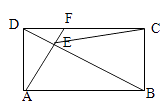
∵AB=4 ![]() ,AD=2
,AD=2 ![]() ,∴BD=
,∴BD= ![]() =10.
=10.
∴ ![]() ,BE=
,BE= ![]() =8,cos∠CBE=
=8,cos∠CBE= ![]() =
= ![]() .
.
在△BCE中,由余弦定理得CE= ![]() =2
=2 ![]() .
.
∵θ=90°,∴A′E⊥平面ABCD,∴A′E⊥CE.
∴|A′C|= ![]() =2
=2 ![]() .
.
(2)DE= ![]() =2.
=2.
∵tan∠FDE= ![]() ,∴EF=1,DF=
,∴EF=1,DF= ![]() =
= ![]() .
.
当 ![]() 即cos∠A′EF=
即cos∠A′EF= ![]() 时,
时, ![]() .
.
∴A′E2=A′F2+EF2,∴∠A'FE=90°
又BD⊥AE,BD⊥EF,∴BD⊥平面A'EF,∴BD⊥A'F
∴A'F⊥平面ABCD.
以F为原点,以FC为x轴,以过F的AD的平行线为y轴,以FA′为z轴建立空间直角坐标系如图所示:
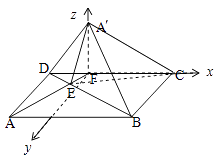
∴A′(0,0, ![]() ),D(﹣
),D(﹣ ![]() ,0,0),B(3
,0,0),B(3 ![]() ,2
,2 ![]() ,0),C(3
,0),C(3 ![]() ,0,0).
,0,0).
∴ ![]() =(0,2
=(0,2 ![]() ,0),
,0), ![]() =(4
=(4 ![]() ,2
,2 ![]() ,0),
,0), ![]() =(
=( ![]() ,0,
,0, ![]() ).
).
设平面A′BD的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 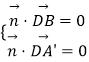 ,
,
∴ ![]() ,令z=1得
,令z=1得 ![]() =(﹣
=(﹣ ![]() ,2
,2 ![]() ,1).
,1).
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() .
.
∴BC与平面A'BD所成角的正弦值为 ![]() .
.
【解析】(1)根据题意作出辅助线利用勾股定理可得AE、CE再由A′E⊥CE得出结果。(2)利用余弦定理可得A ' F的值,从而得出A'F⊥平面ABCD,建立空间直角坐标系如图所示,求出向量CB和平面A′BD的法向量,根据两个向量的数量积公式求出BC与平面A'BD所成角的正弦值即可。
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则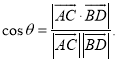 .
.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案