题目内容
在直线x-y-2=0上求一点P,使它与点A(-1,1)、B(1,1)的连线所夹的角∠APB最大.
解析:|AB|=2,又AB的中点M到直线的距离d=![]() >
>![]() ,故直线x-y-2=0必在以AB为直径的圆外,所以∠APB必为锐角.
,故直线x-y-2=0必在以AB为直径的圆外,所以∠APB必为锐角.
设P(x0,x0-2),则
tanAPB=
|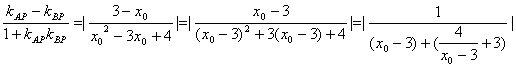 .
.
∵∠APB最大时,|x0-3|+![]() 取最小值4,而此时|x0-3|=
取最小值4,而此时|x0-3|=![]() ,
,
∴x0=1,点P(1,-1).

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
题目内容
在直线x-y-2=0上求一点P,使它与点A(-1,1)、B(1,1)的连线所夹的角∠APB最大.
解析:|AB|=2,又AB的中点M到直线的距离d=![]() >
>![]() ,故直线x-y-2=0必在以AB为直径的圆外,所以∠APB必为锐角.
,故直线x-y-2=0必在以AB为直径的圆外,所以∠APB必为锐角.
设P(x0,x0-2),则
tanAPB=
|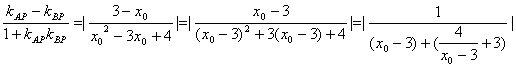 .
.
∵∠APB最大时,|x0-3|+![]() 取最小值4,而此时|x0-3|=
取最小值4,而此时|x0-3|=![]() ,
,
∴x0=1,点P(1,-1).

 新思维寒假作业系列答案
新思维寒假作业系列答案