Question

函数f（x）=

1nx

x

（1≤x≤e²）与函数g（x）=kx恒有两不同的交点，则k的取值范围是

 

．

Answer 1

分析：函数f（x）=

1nx

x

（1≤x≤e²）与函数g（x）=kx恒有两不同的交点，?lnx=kx²（1≤x≤e²）由两个不同交点．分别作出函数g（x）=lnx，（1≤x≤e²），h（x）=kx²的图象．由图象可知：k＞0．利用函数g（x）=lnx，在[1，e²]上单调性，当函数h（x）=kx²经过点（e²，2）时，满足题意，利用点M的坐标得出此时的k的值．
②利用导数再求出函数函数g（x）=lnx，（1≤x≤e²），h（x）=kx²的图象相切时的切点P（x₀，y₀）的横坐标即可得出k的取值范围．

解答：解：函数f（x）=

1nx

x

（1≤x≤e²）与函数g（x）=kx恒有两不同的交点，?lnx=kx²（1≤x≤e²）由两个不同交点．
分别作出函数g（x）=lnx，（1≤x≤e²），h（x）=kx²的图象．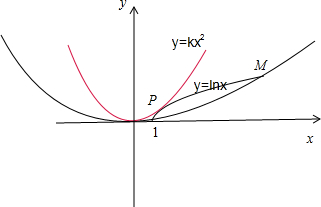
由图象可知：k＞0．
①函数g（x）=lnx，在[1，e²]上单调递增，∴lnx∈[0，2]．
当函数h（x）=kx²经过点（e²，2）时，满足题意，此时ke²=2，解得k=

2

e2

．
②假设函数函数g（x）=lnx，（1≤x≤e²），h（x）=kx²的图象相切于点P（x₀，y₀）．
∵g′(x)=

1

x

，h′（x）=2kx．
∴

1

x0

=2kx0，化为2k

x

2 0

=1．
又k

x

2 0

=lnx0=y0，
∴2lnx₀=1，解得x0=

e

．
∴k=

1

2 x 2 0

=

1

2e

．
∴当

1

2e

＜k≤

2

e2

时，满足函数f（x）=

1nx

x

（1≤x≤e²）与函数g（x）=kx恒有两不同的交点．
故答案为(

1

2e

，

2

e2

]．

点评：本题考查了函数的图象与性质、利用导数研究函数的切线的斜率问题、恒成立问题的等价转化、数形结合等基础知识与基本技能方法，属于难题．