题目内容
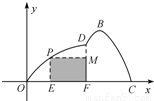 如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<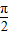 ),x∈[4,8]时的图象,图象的最高点为B(5,
),x∈[4,8]时的图象,图象的最高点为B(5,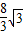 ),DF⊥OC,垂足为F.
),DF⊥OC,垂足为F.(I)求函数y=Asin(ωx+φ)的解析式;
(II)若在湖泊内修建如图所示的矩形水上乐园PMFE,问点P落在曲线OD上何处时,水上乐园的面积最大?
【答案】分析:(I)利用函数的解析式,结合函数的图象求出A,ω,通过函数经过B,求出φ,即可求函数y=Asin(ωx+φ)的解析式;
(II)求出D(4,4),曲线OD的方程为y2=4x,(0≤x≤4).推出矩形的面积的表达式,利用函数的导数求出面积的最大值,推出P的位置即可.
解答:解:(Ⅰ)对于函数y=Asin(ωx+φ)由图象可知,A= ,ω=
,ω= =
= ,
,
将(5, ),代入y=
),代入y= sin(
sin( x+φ)得:
x+φ)得: ,
,
|φ|< ,所以φ=
,所以φ= ,所以函数的解析式为y=
,所以函数的解析式为y= sin(
sin( x
x ).
).
(Ⅱ)在y= sin(
sin( x
x )中,令x=4,得D(4,4)
)中,令x=4,得D(4,4)
从而得曲线OD的方程为y2=4x,(0≤x≤4).
设点P( )(0≤t≤4),则矩形PMFE的面积为S=
)(0≤t≤4),则矩形PMFE的面积为S= ,0≤t≤4.
,0≤t≤4.
因为S′=4- ,由S′=0得t=
,由S′=0得t= ,且t∈
,且t∈ 时S′>0,S递增,
时S′>0,S递增,
t∈ 时S′<0,S递减,
时S′<0,S递减,
所以当t= ,S最大,此时点P的坐标
,S最大,此时点P的坐标 .
.
点评:本题考查已知三角函数模型的应用问题,利用导数研究函数的单调性,由y=Asin(ωx+φ)的部分图象确定其解析式,考查分析问题解决问题的能力.
(II)求出D(4,4),曲线OD的方程为y2=4x,(0≤x≤4).推出矩形的面积的表达式,利用函数的导数求出面积的最大值,推出P的位置即可.
解答:解:(Ⅰ)对于函数y=Asin(ωx+φ)由图象可知,A=
 ,ω=
,ω= =
= ,
,将(5,
 ),代入y=
),代入y= sin(
sin( x+φ)得:
x+φ)得: ,
,|φ|<
 ,所以φ=
,所以φ= ,所以函数的解析式为y=
,所以函数的解析式为y= sin(
sin( x
x ).
).(Ⅱ)在y=
 sin(
sin( x
x )中,令x=4,得D(4,4)
)中,令x=4,得D(4,4)从而得曲线OD的方程为y2=4x,(0≤x≤4).
设点P(
 )(0≤t≤4),则矩形PMFE的面积为S=
)(0≤t≤4),则矩形PMFE的面积为S= ,0≤t≤4.
,0≤t≤4.因为S′=4-
 ,由S′=0得t=
,由S′=0得t= ,且t∈
,且t∈ 时S′>0,S递增,
时S′>0,S递增,t∈
 时S′<0,S递减,
时S′<0,S递减,所以当t=
 ,S最大,此时点P的坐标
,S最大,此时点P的坐标 .
.点评:本题考查已知三角函数模型的应用问题,利用导数研究函数的单调性,由y=Asin(ωx+φ)的部分图象确定其解析式,考查分析问题解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011•盐城二模)如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
(2011•盐城二模)如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<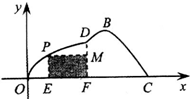 如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< ),x∈[4,8]时的图象,图象的最高点为B(5,
),x∈[4,8]时的图象,图象的最高点为B(5, ),DF⊥OC,垂足为F.
),DF⊥OC,垂足为F.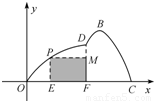 如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<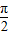 ),x∈[4,8]时的图象,图象的最高点为B(5,
),x∈[4,8]时的图象,图象的最高点为B(5,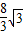 ),DF⊥OC,垂足为F.
),DF⊥OC,垂足为F.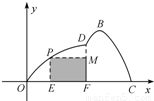 如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<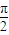 ),x∈[4,8]时的图象,图象的最高点为B(5,
),x∈[4,8]时的图象,图象的最高点为B(5,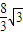 ),DF⊥OC,垂足为F.
),DF⊥OC,垂足为F.