题目内容
设 ,
,
(1)若 为偶函数,求实数
为偶函数,求实数 的值;
的值;
(2)记 的最小值为
的最小值为 ,求
,求 的表达式.
的表达式.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)方法一:因为 为偶函数,所以
为偶函数,所以 恒成立,带入原函数式,解得
恒成立,带入原函数式,解得 ;方法二:因为
;方法二:因为 为偶函数,所以
为偶函数,所以 ;(2)将原函数分类讨论的思想去绝对值,分别化为二次函数,进一步分别求最小值,得到
;(2)将原函数分类讨论的思想去绝对值,分别化为二次函数,进一步分别求最小值,得到 的表达式.
的表达式.
试题解析:(1) 为偶函数
为偶函数 恒成立,
恒成立,
即
 . 3分
. 3分
(2)当 时,
时, ,对称轴为
,对称轴为
若 即
即 时,
时,
若 即
即 时,
时, . 6分
. 6分
当 时,
时, ,对称轴为
,对称轴为 .
.
若 即
即 时,
时, .
.
若 即
即 时,
时, . 9分
. 9分
 时,
时,
 .
.
 时,
时,
 . 11分
. 11分
 . 13分
. 13分
考点:1.偶函数的性质;2.分类讨论去绝对值;3.二次函数求最小值.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 中,
中, 和
和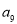 是关于方程
是关于方程 的两根,则该数列的前11项和
的两根,则该数列的前11项和 ( )
( )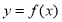 的定义域为[1,5],则函数
的定义域为[1,5],则函数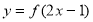 的定义域是( )
的定义域是( ) 在区间
在区间 上单调递减,那么实数
上单调递减,那么实数 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.
 为偶函数,对任意的
为偶函数,对任意的 都有
都有 成立,则
成立,则 由大到小的顺序为 .[
由大到小的顺序为 .[ 是方程
是方程 的解,则
的解,则 B.
B. C.
C. D.
D.
 ,在
,在 轴、
轴、 轴上的截距分别为
轴上的截距分别为 ,且满足
,且满足 的直线方程为 .
的直线方程为 . ,定义
,定义 为
为 ,则数列
,则数列