Question

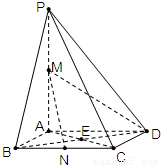
（文科）如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PA⊥底面ABCD，PA=4，M为PA的中点，N为BC的中点．
（1）求四棱锥P-ABCD的体积；
（2）求异面直线PC与MD所成角的大小．

Answer 1

【答案】分析：（1）由于底面是正方形，PA⊥底面ABCD，直接利用四棱锥的体积公式可以计算；
（2）连ME，则ME∥PC，因此∠EMD即为异面直线MD与PC所成角通过计算可得．
解答：解：（1）根据棱锥的体积公式有==；
（公式（2分），结果2分）
（2）连ME，则ME∥PC，因此∠EMD即为异面直线MD与PC所成角．   （3分）
计算得
所以=，∠EMD=30°（8分）
（公式（2分），结果3分）
即：异面直线PC与MD所成角为30°．
点评：本题的考点是异面直线及其所成的角，主要考查四棱锥的体积计算即异面直线所成角的计算，属于基础题