题目内容
如图,在斜三棱柱ABC-A1B1C1中,AC=BC,D为AB的中点,平面A1B1C1⊥平面ABB1A1,异面直线BC1与AB1相互垂直.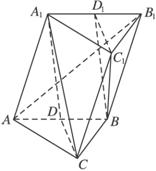
(1)求证AB1⊥平面A1CD;
(2)若CC1与平面ABB1A1的距离为1,A1C=![]() ,AB1=5,求三棱锥A1-ACD的体积.
,AB1=5,求三棱锥A1-ACD的体积.
(1)证明:取A1B1的中点D1,连结C1D1、BD1,
∴AC=BC,

∴A1C1=B1C1.
又C1D1⊥A1B1,平面A1B1C1⊥平面ABB1A1,
∴C1D1⊥平面ABB1A1.∴BD1是BC1在平面ABB1A1内的射影,BC1⊥AB1,所以AB1⊥BD1.又BD1∥A1D,∴AB1⊥A1D.
 CD⊥平面A1B1BA,
CD⊥平面A1B1BA,
从而CD⊥AB1.
∴AB1⊥平面A1CD.
(2)解析:由(1)知CD是CC1与平面ABB1A1的距离,
∴CD=1.
在Rt△A1CD中,A1C=![]() ,CD=1,
,CD=1,
∴A1D=![]() =6.
=6.
设A1D∩AB1=E,由△AED∽△B1EA1,得
![]() =
=![]() ,∴AE=
,∴AE=![]() AB1=
AB1=![]() ,
,
![]() =
=![]() A1D·AE=
A1D·AE=![]() ×6×
×6×![]() =5.
=5.
![]() ·CD=
·CD=![]() ×5×1=
×5×1=![]() .
.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
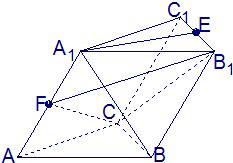 如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点
如图,在斜三棱柱ABC-A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120°,E、F分别是棱B1C1、A1A的中点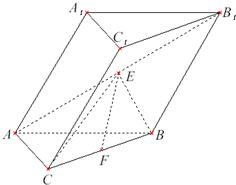 如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.  如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( )
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,又BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H一定在( )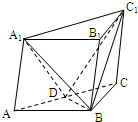 (2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点.
(2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点. (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=