题目内容
已知函数![]() (其中常数
(其中常数![]() ).
).
(1)求![]() 的单调区间;
的单调区间;
(2)若存在实数![]() ,使得对任意
,使得对任意![]() ,不等式
,不等式![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围,若不存在,请说明理由。
的取值范围,若不存在,请说明理由。
解:(1)函数![]() 的定义域为
的定义域为![]()
![]()
由![]() ,解得
,解得![]() ,由
,由![]() ,解得
,解得![]() 且
且![]()
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() 和
和![]() 5分
5分
(2)假设存在这样实数![]() ,使得对任意
,使得对任意![]() ,不等式
,不等式![]() 恒成立。
恒成立。
∵![]() ∴
∴![]() ∴
∴![]()
由![]() ① 8分
① 8分
设![]()
![]()
![]()
![]()
∴![]()
∴![]() ② 11分
② 11分
由①、②可知,不存在符合题设条件的实数![]() 12分
12分

练习册系列答案
相关题目
 (其中常数a,b∈R),
(其中常数a,b∈R), .
. 时,求函数g(x)在[0,a]上的最小值h(a),并探索:是否存在满足条件的实数a,使得对任意的x∈R,f(x)>h(a)恒成立.
时,求函数g(x)在[0,a]上的最小值h(a),并探索:是否存在满足条件的实数a,使得对任意的x∈R,f(x)>h(a)恒成立.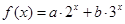 ,其中常数
,其中常数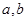 满足
满足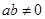 。
。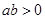 ,判断函数
,判断函数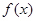 的单调性;
的单调性;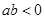 ,求
,求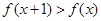 时
时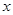 的取值范围。
的取值范围。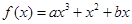 (其中常数
(其中常数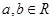 ),
),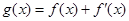 是奇函数。
是奇函数。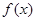 的表达式;
的表达式;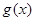 的单调性,并求
的单调性,并求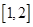 上的最大值和最小值。
上的最大值和最小值。