Question

数列{a_n}满足a₁=1,a_n+1=(n²+n－λ)a_n (n=1,2,···)，λ是常数.

（Ⅰ）当a₂=-1时，求λ及a₃的值；

（Ⅱ）数列{a_n}是否可能为等差数列？若可能，求出它的通项公式；若不可能，说明理由；

（Ⅲ）求λ的取值范围，使得存在正整数m,当n＞m时总有a_n＜0.

Answer 1

解：（Ⅰ）由于且a₁=1，

              所以当a₂=-1时，得,

              故

            　从而

　（Ⅱ）数列{a_n}不可能为等差数列.证明如下：

            　由a₁=1，得

　　     　

            　若存在，使｛a_n｝为等差数列，则a₃-a₂=a₂-a₁,即

            　

            　解得=3.

              于是

　　　　　这与｛a_n｝为等差数列矛盾，所以，对任意，{a_n}都不可能是等差数列.

（Ⅲ）记根据题意可知，b₁＜0且，即＞2且N*)，这时总存在N*，满足：当n≥n₀时，b_n＞0；当n≤n₀-1时，b_n＜0.

　　　　所以由a_n+1=b_na_n及a₁=1＞0可知，若n₀为偶数，则，从而当n＞n₀

时a_n＜0；若n₀为奇数，则，从而当n＞n₀时a_n＞0.

因此“存在mN*，当n＞m时总有a_n＜0”的充分必要条件是：n_o为偶数，

记n_o=2k(k=1,2, …)，则满足

                    

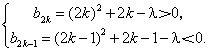
故的取值范围是4k²+2k(kN*).