题目内容
已知函数 ,
, ,
, .
.
(1)若 ,试判断并证明函数
,试判断并证明函数 的单调性;ww
的单调性;ww
(2)当 时,求函数
时,求函数 的最大值的表达式
的最大值的表达式 .
.
解:(1)判断:若 ,函数
,函数 在
在 上是增函数.
上是增函数.
证明:当 时,
时, ,
,
在区间 上任意
上任意 ,设
,设 ,
,

所以 ,即
,即 在
在 上是增函数.
上是增函数.
(注:用导数法证明或其它方法说明也同样给5分) www.zxs
(2)因为 ,所以
,所以
①当 时,
时, 在
在 上是增函数,在
上是增函数,在 上也是增函数,
上也是增函数,
所以当 时,
时, 取得最大值为
取得最大值为 ;
;
②当 时,
时, 在
在 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,
在 上是增函数,
上是增函数,
而 ,
,
当 时,
时, ,当
,当 时,函数
时,函数 取最大值为
取最大值为 ;
;
当 时,
时, ,当
,当 时,函数
时,函数 取最大值为
取最大值为 ;
;
综上得,

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 的内角
的内角 所对的边是
所对的边是 ,且
,且
 ;
;  的值.
的值.  ,若实数
,若实数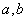 满足
满足 ,则
,则 ______
______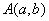 ,
,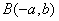 在函数
在函数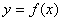 的图象上,则称
的图象上,则称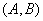 是函数
是函数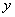 轴
轴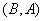 视为同一组), 则函数
视为同一组), 则函数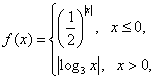 关于
关于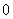 B.
B.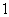 C.
C.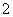 D.
D.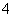
 和
和 ,定义
,定义 ,若平面向量
,若平面向量 满足:
满足: ,
, 与
与 的夹角
的夹角 ,且
,且 和
和 都在集合
都在集合 中,
中, .
. ,那么它的体积为
,那么它的体积为 B.
B. C.
C.  D.
D. 

 ,若将函数
,若将函数 的图像向左平移
的图像向左平移 个单位后所得图像与原图像重合,则
个单位后所得图像与原图像重合,则 的值不可能为( )
的值不可能为( ) 尺 B.
尺 B. 尺 C.
尺 C. 尺 D.
尺 D. 尺
尺