题目内容
已知动圆x2+y2-2ax-ay+a2=0(a≠0),(Ⅰ)求动圆圆心P的轨迹方程；
(Ⅱ)证明直线：4x-3y=0和y=0是该方程所表示的所有圆的公切线；
(Ⅲ)画出图形表示第(Ⅰ)、(Ⅱ)两小题的结论，要求图中至少有两个圆.
解：(Ⅰ)设圆心为P(x,y)，将已知圆的方程配方得圆心为(a,
)
∴
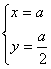
x-2y=0(x≠0)为轨迹方程.
(Ⅱ)(a,
)到y=0,4x-3y=0的距离都为
,故x轴，4x-3y=0是所有圆的公切线.
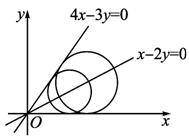
(Ⅲ)图示如图.
练习册系列答案
相关题目