题目内容
数列{an}满足a1=1,a2=2,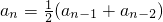 ,(n=3,4,…);数列{bn}是首项为b1=1,公比为-2的等比数列.
,(n=3,4,…);数列{bn}是首项为b1=1,公比为-2的等比数列.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=nanbn(n=1,2,3,…),求数列{cn}的前n项和Sn.
解:(Ⅰ)由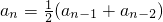 ,
,
得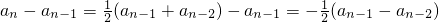 ,(n≥3)(2分)
,(n≥3)(2分)
又∵a2-a1=1≠0,
∴数列{an+1-an}是首项为1公比为 的等比数列,
的等比数列,
∴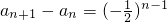 .
.
an=a1+(a2-a1)+(a3-a2)+(a4-a3)+…+(an-an-1)
=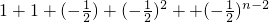
=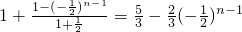 ,(4分)
,(4分)
经检验它对n=1,2也成立,
∴数列{an}的通项公式为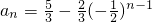 (5分)
(5分)
∵数列{bn}是首相为b1=1,
公比为-2的等比数列.
∴bn=1×(-2)n-1=(-2)n-1.(7分)
(Ⅱ)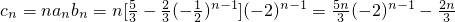 ,
,
Sn=c1+c2+c3+…+cn=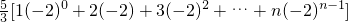 -
-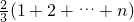
=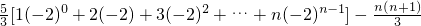 (10分),
(10分),
记Tn=1•(-2)0+2•(-2)+3•(-2)2+…+n•(-2)n-1,①
则2Tn=1•(-2)1+2•(-2)2+…+(n-1)•(-2)n-1+n•(-2)n②,
由①-②得:-Tn=(-2)0+(-2)+(-2)2+…+(-2)n-1-n•(-2)n
=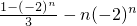 ,
,
∴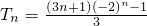 (12分)
(12分)
∴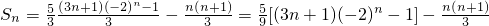 (14分)
(14分)
分析:(Ⅰ)由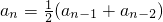 得
得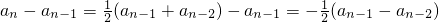 ,(n≥3).由此能导出数列{an}的通项公式.由数列{bn}是首相为b1=1,公比为-2的等比数列,能求出{bn}的通项公式.
,(n≥3).由此能导出数列{an}的通项公式.由数列{bn}是首相为b1=1,公比为-2的等比数列,能求出{bn}的通项公式.
(Ⅱ)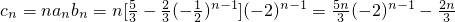 ,记Tn=1•(-2)0+2•(-2)+3•(-2)2++n•(-2)n-1,由错位相减法能导出
,记Tn=1•(-2)0+2•(-2)+3•(-2)2++n•(-2)n-1,由错位相减法能导出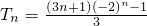 ,由此能求出数列{cn}的前n项和Sn.
,由此能求出数列{cn}的前n项和Sn.
点评:本题考查数列的性质和应用,解题时要注意挖掘题设中的隐含条件.
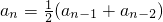 ,
,得
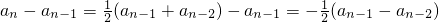 ,(n≥3)(2分)
,(n≥3)(2分)又∵a2-a1=1≠0,
∴数列{an+1-an}是首项为1公比为
 的等比数列,
的等比数列,∴
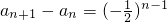 .
.an=a1+(a2-a1)+(a3-a2)+(a4-a3)+…+(an-an-1)
=
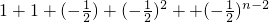
=
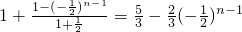 ,(4分)
,(4分)经检验它对n=1,2也成立,
∴数列{an}的通项公式为
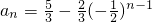 (5分)
(5分)∵数列{bn}是首相为b1=1,
公比为-2的等比数列.
∴bn=1×(-2)n-1=(-2)n-1.(7分)
(Ⅱ)
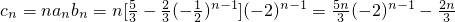 ,
,Sn=c1+c2+c3+…+cn=
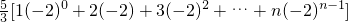 -
-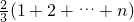
=
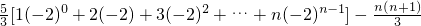 (10分),
(10分),记Tn=1•(-2)0+2•(-2)+3•(-2)2+…+n•(-2)n-1,①
则2Tn=1•(-2)1+2•(-2)2+…+(n-1)•(-2)n-1+n•(-2)n②,
由①-②得:-Tn=(-2)0+(-2)+(-2)2+…+(-2)n-1-n•(-2)n
=
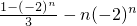 ,
,∴
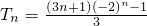 (12分)
(12分)∴
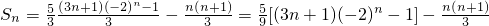 (14分)
(14分)分析:(Ⅰ)由
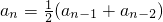 得
得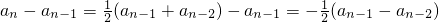 ,(n≥3).由此能导出数列{an}的通项公式.由数列{bn}是首相为b1=1,公比为-2的等比数列,能求出{bn}的通项公式.
,(n≥3).由此能导出数列{an}的通项公式.由数列{bn}是首相为b1=1,公比为-2的等比数列,能求出{bn}的通项公式.(Ⅱ)
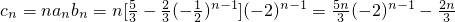 ,记Tn=1•(-2)0+2•(-2)+3•(-2)2++n•(-2)n-1,由错位相减法能导出
,记Tn=1•(-2)0+2•(-2)+3•(-2)2++n•(-2)n-1,由错位相减法能导出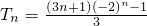 ,由此能求出数列{cn}的前n项和Sn.
,由此能求出数列{cn}的前n项和Sn.点评:本题考查数列的性质和应用,解题时要注意挖掘题设中的隐含条件.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目