题目内容
【题目】已知数列![]() 中,
中, ![]() ,且
,且![]() 对任意正整数
对任意正整数![]() 都成立,数列
都成立,数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() ;
;
(2)是否存在实数![]() ,使数列
,使数列![]() 是公比为1的等比数列,且任意相邻三项
是公比为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有
按某顺序排列后成等差数列,若存在,求出所有![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若![]() ,求
,求![]() .(用
.(用![]() 表示).
表示).
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) 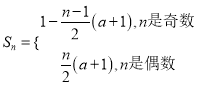 .
.
【解析】试题分析:
(1)由题意求得首项![]() ,公差
,公差![]() ,结合等差数列前n项和公式列方程可得
,结合等差数列前n项和公式列方程可得![]() ;
;
(2)假设存在满足题意的实数k,分类讨论可得![]() ;
;
(3)结合题意分类讨论,然后分组求和可得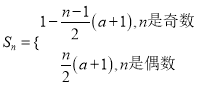 .
.
试题解析:
(1)![]() 时,
时, ![]() ,
,
所以数列![]() 是等差数列,
是等差数列,
此时首项![]() ,公差
,公差![]() ,
,
数列![]() 的前
的前![]() 项和是
项和是![]() ;
;
故![]() ,得
,得![]() ;
;
(2)设数列![]() 是等比数列,则它的公比
是等比数列,则它的公比![]() ,所以
,所以![]() ,
,
①![]() 为等差中项,则
为等差中项,则![]() ,
,
即![]() ,解得
,解得![]() ,不合题意;
,不合题意;
②![]() 为等差中项,则
为等差中项,则![]() ,
,
即![]() ,化简得:
,化简得: ![]() ,解得
,解得![]() 或
或![]() (舍去);
(舍去);
③若![]() 为等差中项,则
为等差中项,则![]() ,
,
即![]() ,化简得:
,化简得: ![]() ,解得
,解得![]() ;
;
![]() ;
;
综上可得,满足要求的实数![]() 有且仅有一个,
有且仅有一个, ![]() ;
;
(3)![]() ,则
,则![]() ,
,
![]() ,
,
当![]() 是偶数时,
是偶数时, ![]()
![]() ,
,
当![]() 是奇数时,
是奇数时, ![]()
![]() ,
,
![]() 也适合上式,
也适合上式,
综上可得, 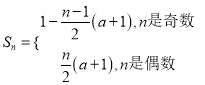 .
.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目