题目内容
已知 ,则线段
,则线段 的中点
的中点 的坐标为 ( )
的坐标为 ( )
 ,则线段
,则线段 的中点
的中点 的坐标为 ( )
的坐标为 ( )A. | B. | C.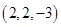 | D. |
B
试题分析:因为P为线段AB的中点,所以由A和B的坐标,利用中点坐标公式即可求出P的坐标.解:由A(3,2,1)、B(1,0,4),P为线段AB的中点,得到P的坐标为(
 ),即(2,1,
),即(2,1, ).故选B.
).故选B.点评:此题考查了线段中点坐标的求法,熟练掌握中点坐标公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
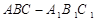 的底面是直角三角形,
的底面是直角三角形, 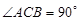 ,侧棱与底面所成角为
,侧棱与底面所成角为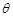 ,点
,点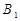 在底面上的射影
在底面上的射影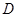 落在
落在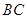 上.
上.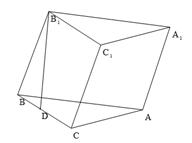
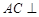 平面
平面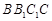 ;
;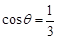 ,且当
,且当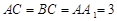 时,求二面角
时,求二面角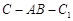 的大小.
的大小. 矩形ABCD所在的平面,M,N分别为AB,PC的中点。求证:
矩形ABCD所在的平面,M,N分别为AB,PC的中点。求证: 平面
平面

 中,
中,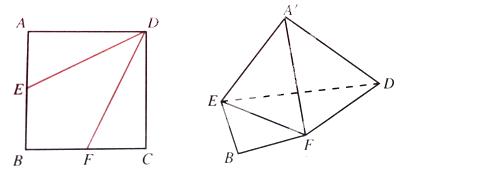
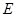 是
是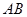 的中点,点
的中点,点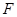 是
是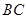 的中点,将
的中点,将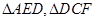 分别沿
分别沿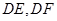 折起,使
折起,使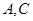 两点重合于点
两点重合于点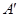 。求证:
。求证: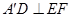
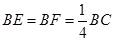 时,求三棱锥
时,求三棱锥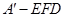 的体积。
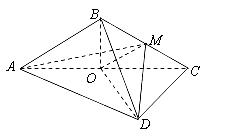
的体积。 的边长为6,
的边长为6, ,
, .将菱形
.将菱形 折起,得到三棱锥 ,点
折起,得到三棱锥 ,点 是棱
是棱 的中点,
的中点, .
.
 ;
; 的体积.
的体积.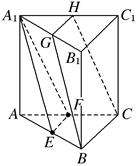

 平面ADE;
平面ADE; 的底面是菱形,且
的底面是菱形,且 面
面 ,
, ,
, ,
, 为棱
为棱 的中点,
的中点, 为线段
为线段 的中点,
的中点,
 面
面 与平面
与平面 的位置关系,并证明你的结论;
的位置关系,并证明你的结论; 的体积.
的体积.